この記事は2024年3月現在のGeoGebra公式サイトをもとに作成しています。
この記事ではGeoGebraの組み込み関数と演算子について説明しています。GeoGebraにはたくさんの関数や演算子が実装されており、さまざまな数学的演算を行うことができます。組み込み関数や演算子について学ぶことで、GeoGebraをさらに使いこなすことができるようになるでしょう。
組み込み関数および演算子のリスト
定数など
| 演算/関数 | 入力方法 |
| ℯ (ネイピア数) | Alt + e |
| ί (虚数単位) | Alt + i |
| π(円周率) | Alt + p or pi |
| °(角度の「°」) | Alt + o or deg |
四則演算、べき乗、階乗など
| 演算/関数 | 入力方法 |
| 加算 | + |
| 減算 | – |
| 乗算 | * or Space key |
| スカラー積(内積) | * or Space key |
| ベクトル積 (外積) | ⊗ |
| 除算 | / |
| べき乗 | ^ or superscript ( x^2 or x2) |
| 階乗 | ! |
| カッコ | ( ) |
| 絶対値 | abs( ) |
ちなみに、GeoGebraでベクトルや行列を定義するには{ }(中カッコ)を使います。ベクトルや行列を使う方法については別の記事で詳しく説明する予定です。
3次元グラフ関連
3次元グラフ関連の組み込み演算は以下の通りです。
| 演算/関数 | 入力方法 |
| 点やベクトルのx座標を取得する 直線におけるxの係数\(a\)を取得する | x( ) |
| 点やベクトルのy座標を取得する yの係数\(b\)を取得する | y( ) |
| 点やベクトルのz座標を取得する zの係数\(c\)を取得する (ただし、\(c=0\)のときは\(d\)を取得する) | z( ) |
| 偏角 | arg( ) |
| 高度角,仰角 | alt( ) |
なお、コマンドx( ),y( ),z( )はどの種類のオブジェクトに対して作用させるかによって挙動が大きく変化します。コマンドx( ),y( ),z( )を点やベクトルに対して作用させた場合、点やベクトルのx,y,z座標をそれぞれ出力します。
適当な点Aに対してコマンドx( ),y( ),z( )を実行した場合の例は以下の通りです。
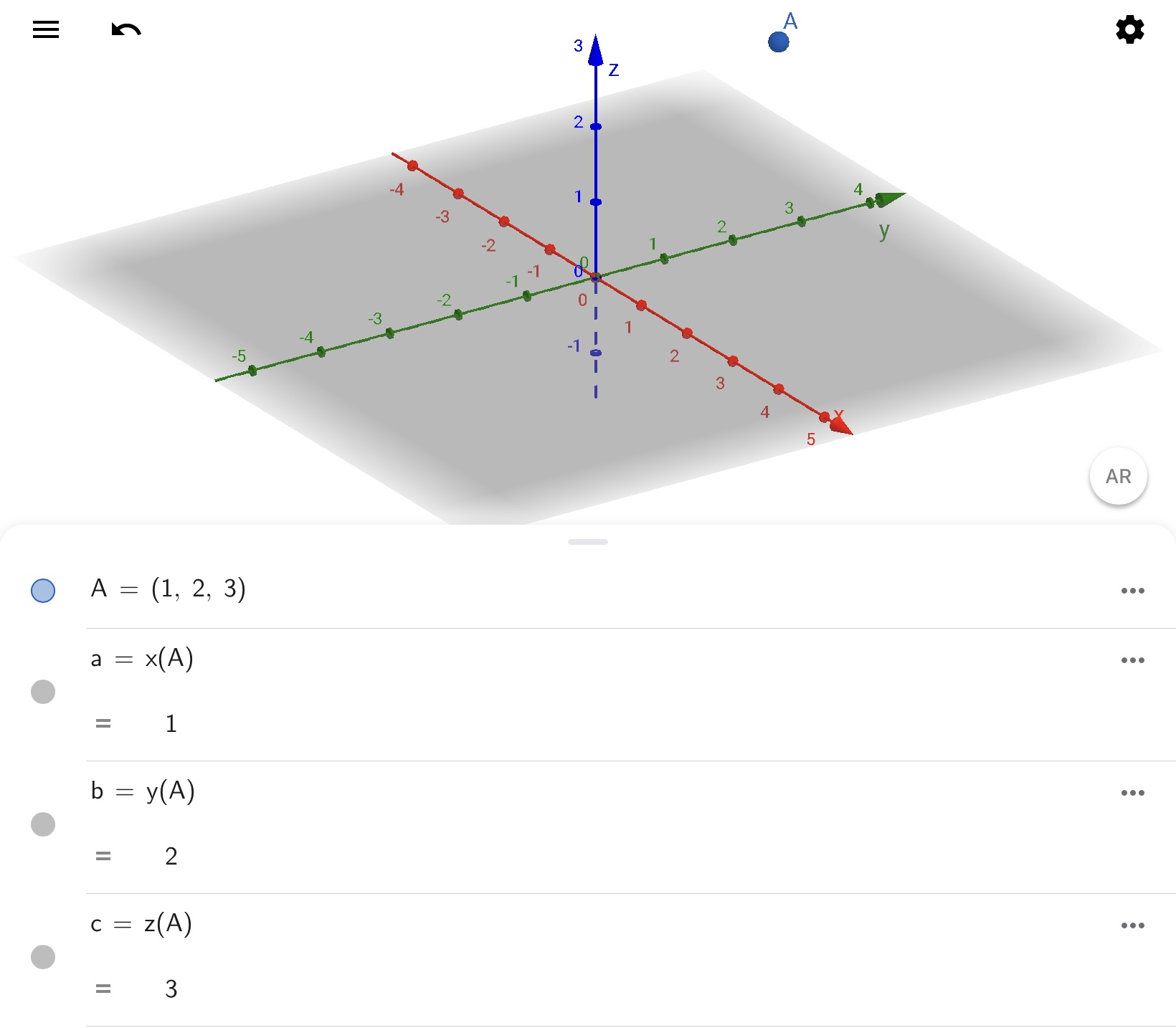
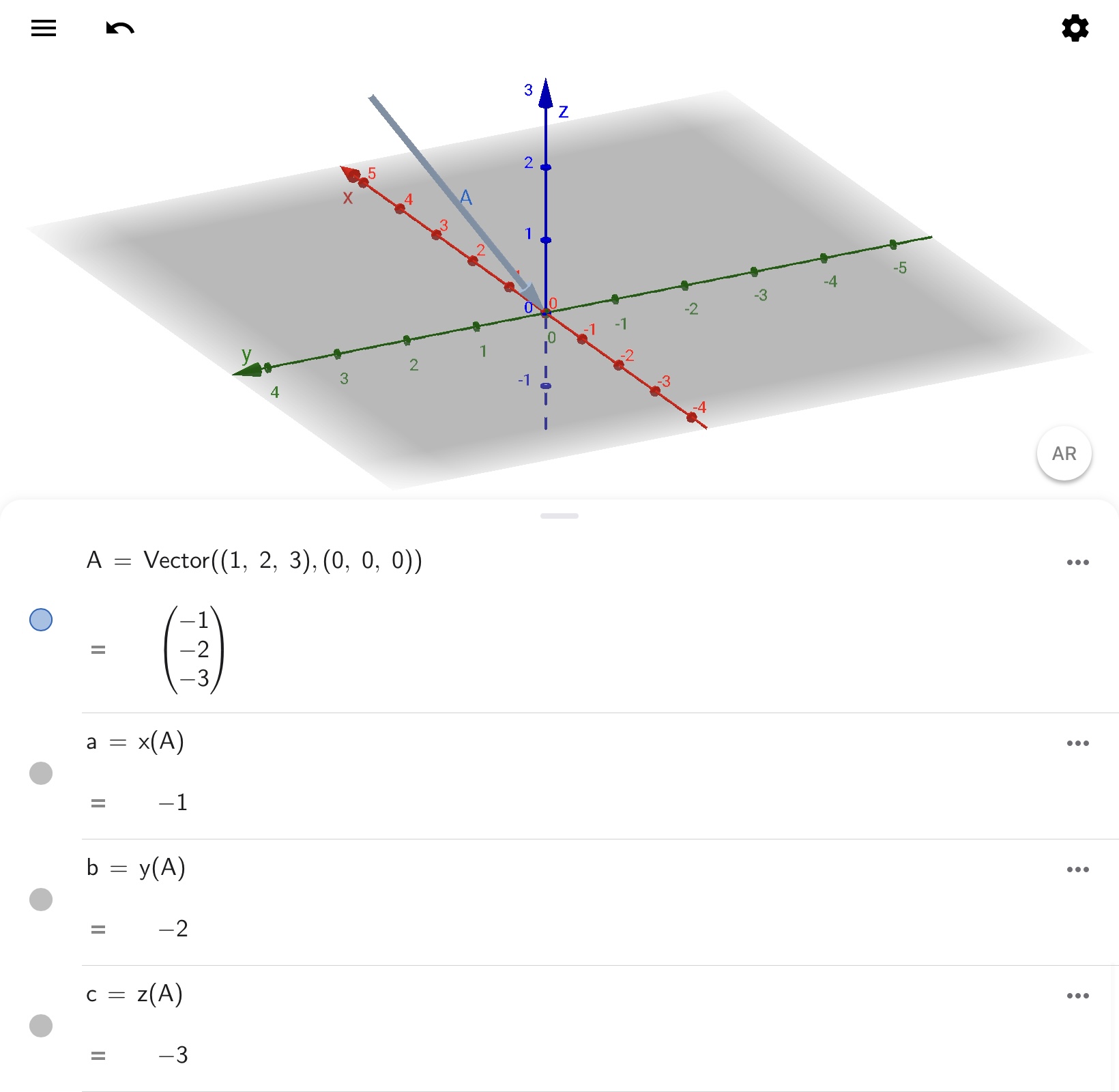
同じように、適当なベクトルAに対してコマンドx( ),y( ),z( )を実行した場合の例は以下の通りです。ベクトルAの各軸方向の成分が抽出されることを確認してください。
\(xyz\)の3次元平面上の直線オブジェクト\(ax+by+cz=d\) (ただし、\(a,b,c,d\)は実数)に対して作用させた場合、変数\(x,y,z\)の係数\(a,b,c\)を取得することができます。使用例を以下に示しますので、ご興味のある方は確認してみてください。
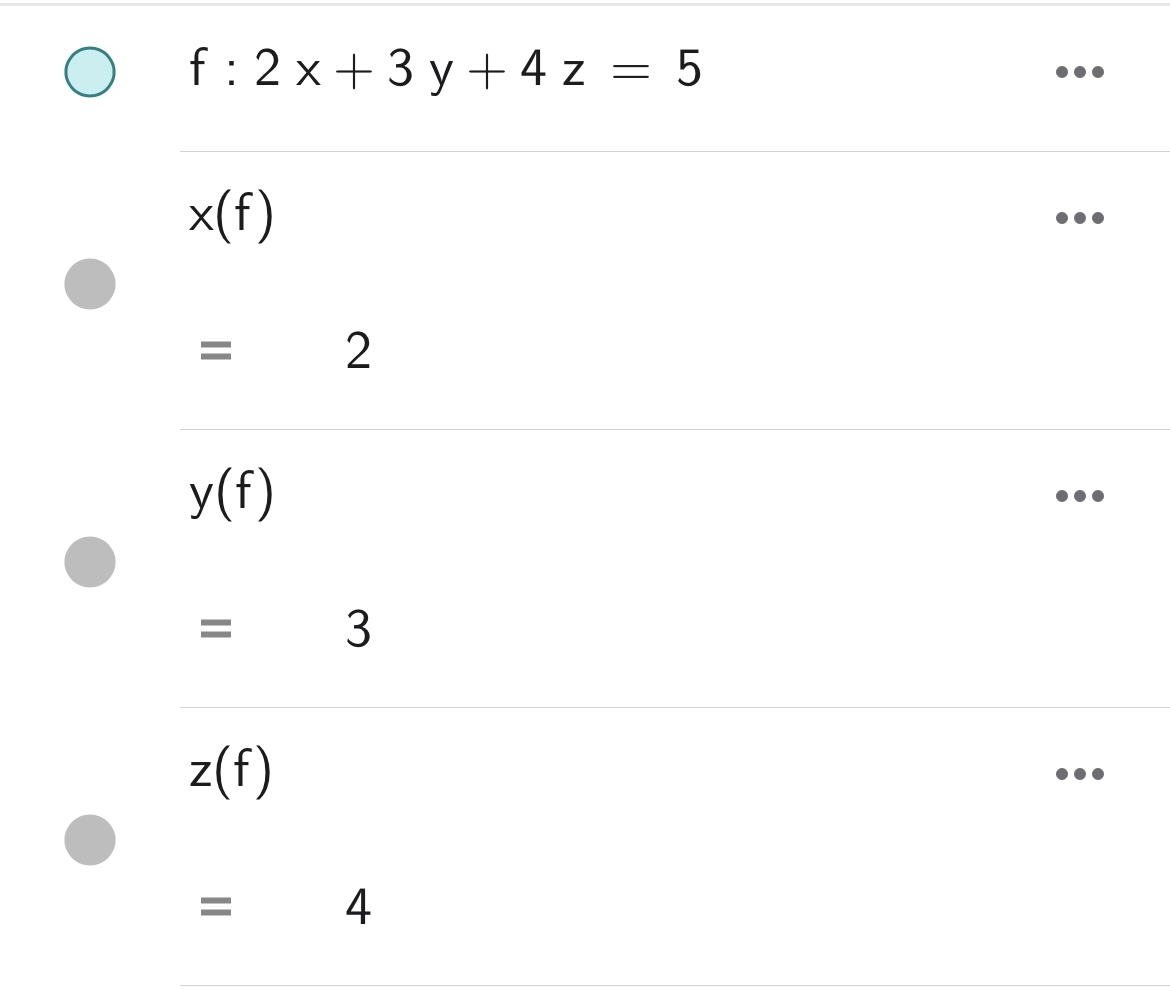
複素数関連
| 演算/関数 | 入力方法 |
| ί (虚数単位) | Alt + i |
| 共役 | conjugate( ) |
| 偏角 | arg( ) |
| 絶対値 | abs( ) |
| 実数部分 | real( )もしくはx( ) |
| 虚数部分 | imaginary( )もしくはy( ) |
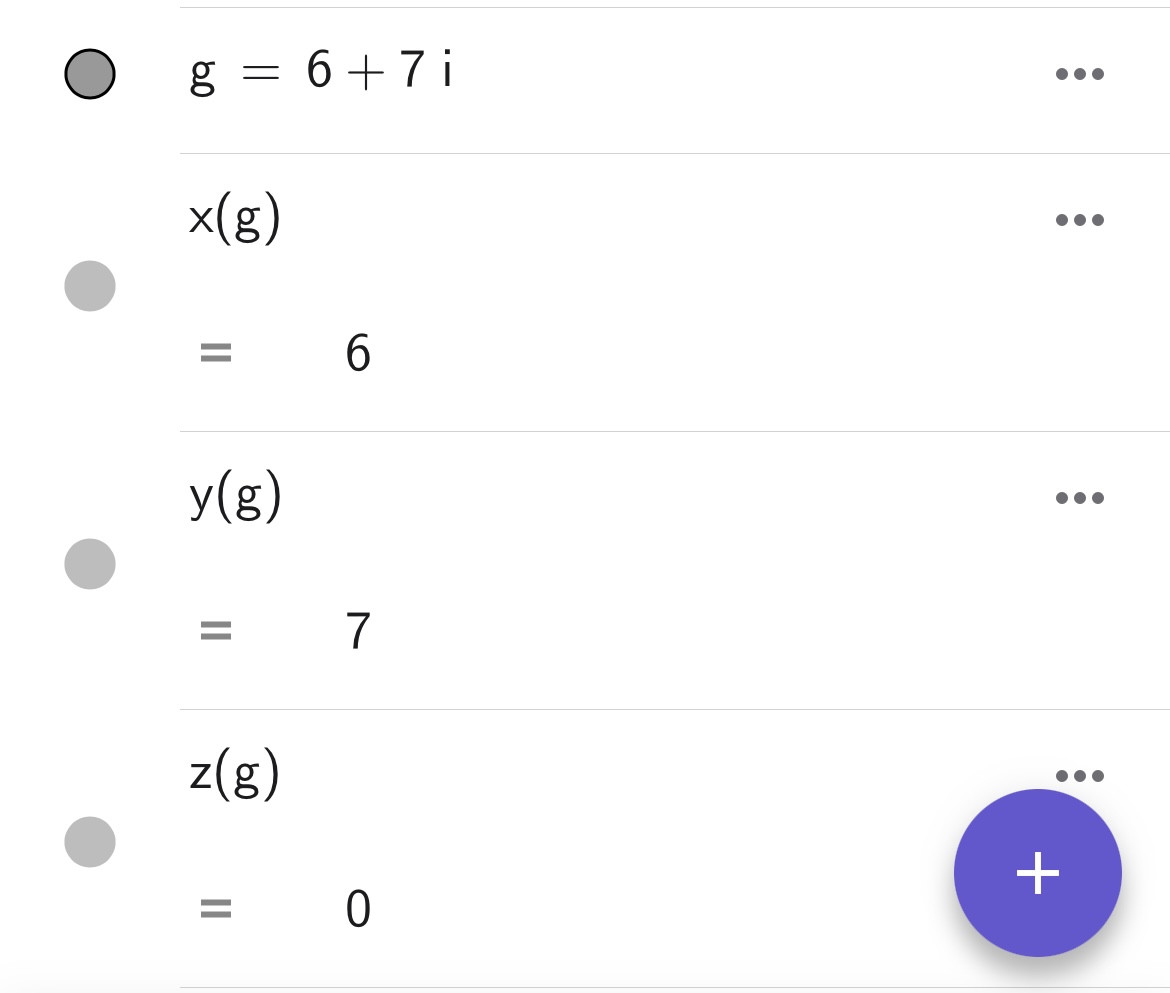
コマンドx( ),y( )を複素数オブジェクトに対して実行した場合、それぞれ実数部分と虚数部分を取得することができます。複素数オブジェクトに対するxyzコマンドの使用例を以下に示します。3次元グラフのときと挙動が異なるので注意してください。
符号関数、丸め、乱数など
| 演算/関数 | 入力方法 |
| 符号(正:1,負:-1,0:0) | sgn( ) or sign() |
| 絶対値 | abs( ) |
| 床関数(自分以下の最大の整数) | floor( ) |
| 天井関数(自分以上の最小の整数) | ceil( ) |
| 最も近い整数に四捨五入 | round(x) |
| 小数点以下y桁に四捨五入 | round(x, y) |
| 0と1の間の乱数 | random( ) |
平方根、指数関数、対数関数など
| 演算/関数 | 入力方法 |
| 平方根 | sqrt( ) |
| 立方根 | cbrt( ) |
| xのn乗根 | nroot(x, n) |
| べき乗(指数関数) | ^ or superscript ( x^2 or x2) |
| ℯ (ネイピア数) | Alt + e |
| 底をeとする指数関数 | exp( ) または ℯx |
| x の底 b に対する対数関数 | log(b, x ) |
| 底がeの対数関数(自然対数) | ln( ) |
| 底が2の対数関数 | log₂() または ld( ) |
| 底が10の対数関数 | log₁₀( ) または log( ) or lg( ) |
三角関数
| 演算/関数 | 入力方法 | 補足 |
| °(角度の「°」) | Alt + o or deg | |
| コサイン | cos( ) | |
| サイン | sin( ) | |
| タンジェント | tan( ) | |
| コセカント | csc() または cosec() | =1/cos( ) |
| セカント | sec() | =1/sin( ) |
| コタンジェント | cot() または cotan() | =1/tan( ) |
| アークコサイン | 弧度法: acos( ) または arccos( ) 度数法: acosd( ) | コサインの逆関数 |
| アークサイン | 弧度法: asin( ) または arcsin( ) 度数法: asind( ) | サインの逆関数 |
| アークタンジェント | 弧度法: atan( ) 度数法: arctan( ) | タンジェントの逆関数 出力範囲: \(-\frac{\pi}{2}\sim + \frac{\pi}{2} \) |
| 4象限アークタンジェント | 弧度法: atan2(y, x) 度数法: atan2d(y, x) | タンジェントの逆関数 出力範囲: \(-\pi \sim +\pi \) |
双曲線関数
| 演算/関数 | 入力方法 | 補足 |
| ハイパボリックコサイン | cosh( ) | |
| ハイパボリックサイン | sinh( ) | |
| ハイパボリックタンジェント | tanh( ) | |
| ハイパボリックコセカント | csch( ) | =1/cosh( ) |
| ハイパボリックセカント | sech( ) | =1/sinh( ) |
| ハイパボリックコタンジェント | coth( ) または cotanh() | =1/tanh( ) |
| 逆双曲線コサイン | acosh( ) または arccosh( ) | |
| 逆双曲線サイン | asinh( ) または arcsinh( ) | |
| 逆双曲線タンジェント | atanh( ) または arctanh( ) |
特殊関数
| 演算/関数 | 入力方法 |
| Beta function Β(a, b) | beta(a, b) |
| Incomplete beta function Β(x;a, b) | beta(a, b, x) |
| Incomplete regularized beta function I(x; a, b) | betaRegularized(a, b, x) |
| Gamma function Γ(x) | gamma( x) |
| (Lower) incomplete gamma function γ(a, x) | gamma(a, x) |
| (Lower) incomplete regularized gamma function P(a,x) = γ(a, x) / Γ(a) | gammaRegularized(a, x) |
| Gaussian Error Function | erf(x) |
| Digamma function | psi(x) |
| The Polygamma function is the (m+1)th derivative of the natural logarithm of the Gamma function, gamma(x) (m=0,1) | polygamma(m, x) |
| The Sine Integral function | sinIntegral(x) |
| The Cosine Integral function | cosIntegral(x) |
| The Exponential Integral function | expIntegral(x) |
| The Riemann-Zeta function ζ(x) | zeta(x) |
| Lambert’s W function LambertW(x, branch) | LambertW(x, 0), LambertW(x, -1) |
まとめ
この記事ではGeoGebraの組み込み関数と演算子について説明しました。ぜひGeoGebraでこれらのコマンドを使ってみてくださいね。
なお、このページではGeoGebraの論理演算子について触れませんでしたが、GeoGebraの論理演算子は下記のページで説明しています。こちらのページも読んでいただければ幸いです。










[…] GeoGebraの組み込み関数と演算子を学ぼう この記事は2024年3月現在のGeoGebra公式サイトをもとに作成しています。 この記事ではGeoGebraの組み込み関数と演… GeoGebra グラフ計算機 コンピュ […]
[…] GeoGebraの組み込み関数と演算子を学ぼう この記事は2024年3月現在のGeoGebra公式サイトをもとに作成しています。 この記事ではGeoGebraの組み込み関数と演… […]
[…] GeoGebraの組み込み関数と演算子を学ぼう この記事は2024年3月現在のGeoGebra公式サイトをもとに作成しています。 この記事ではGeoGebraの組み込み関数と演… […]