GeoGebraの論理演算子を学ぼう

このページではGeoGebraの論理演算子について説明しています。論理演算は数学だけでなく、電子工学や情報工学でも役立つ概念なので、繰り返し勉強してしっかり理解しましょう。

ブール型変数とは？

他の多くのプログラミング言語と同様、GeoGebraではブール型の変数(Boolean、ブーリアン)を扱うことができます。ブール型変数というのは論理演算を取り扱うための専用の変数型で、「true(真)」と「false (偽)」の2値を取り扱います。

入力された命題が成り立つときブール型変数の出力は「true(真)」になり、成り立たないときブール型変数の出力は「false (偽)」になります。

GeoGebraにブール型変数がある理由

一般的なプログラミング言語と同様にGeoGebraにブール型変数が用意されているのは、条件分岐処理や繰り返し処理を行うのにブール型変数があると便利だからです。

唐突ですが、プログラミングの基本3構造は以下の3つです。

1. 順次進行…指示された命令や演算を上から順番に実行する。
2. 条件分岐…特定の条件を満たす場合と満たさない場合とで、異なる処理をする。
3. 繰り返し…同じ動作を繰り返し実行する。ただし、何らかの条件を満たした時、繰り返し処理を停止する。

コンピュータに条件分岐処理や繰り返し処理を行わせようとすると、必ず条件判定が必要になります。条件を満たすときを“true (真)“、条件を満たさないときを“false(偽)“と定義しておくとプログラミングがしやすいため、多くのプログラミング言語ではブール型変数が採用されています。

もちろん、GeoGebraにも条件分岐処理や繰り返し処理のためのコマンドやブール型変数が用意されています。これらのコマンドを使いこなすためには、下記の論理演算子について学ぶことが必須です。

なお、プログラミングの基本3構造についてもっと知りたい方はこの記事がわかりやすいです。→プログラムの基本構造とは？

さまざまな論理演算

変数GeoGebraで取り扱える論理演算のリストは以下の通りです。これらの演算子による演算の結果はすべてブール型変数となります。

演算内容	入力バー	キーボード入力	例	オブジェクトタイプ
Equal (等しい)	≟	==	a ≟ b or a == b	numbers, points, lines, conics, functions (needs CAS), planes, a, b
Not equal (等しくない)	≠	!=	a ≠ b or a != b	numbers, points, lines, conics, functions (needs CAS), planes a, b
Less than (小なり)		<	a < b	numbers a, b
Greater than (大なり)		>	a > b	numbers a, b
Less or equal than (小なりイコール)	≤	<=	a ≤ b or a <= b	numbers a, b
Greater or equal than (大なりイコール)	≥	>=	a ≥ b or a >= b	numbers a, b
And (かつ、論理積)	∧	&&	a ∧ b or a && b	booleans a, b
Or (もしくは、論理和)	∨	||	a ∨ b or a || b	booleans a, b
Not (否定)	¬	!	¬a or !a	boolean a
Exclusive or (排他的論理和)		Alt+	a ⊕ b	booleans a, b
Implication (含意)	→	->	a -> b	booleans a, b
Parallel(平行)	∥		a ∥ b	lines a, b
Perpendicular(垂直)	⊥		a ⊥ b	lines a, b
Belongs to (元として含む、属する)	∈		a ∈ list1	number a, list of numbers list1
Subset (部分集合)	⊆		list1 ⊆ list2	lists list1 and list2
Proper subset (真部分集合)	⊂		list1 ⊂ list2	lists list1 and list2

GeoGebraにはさまざまな機能がありますから、この表だけでは理解が難しいと思います。そのため、もうすこし細かく説明していきたいと思います。

等値演算子、大小関係演算子

もっともオーソドックスな論理演算子は等値演算子と大小関係演算子でしょう。これらの演算子のリストを以下に示します。

演算内容	入力バー	キーボード入力	例
Equal (等しい、イコール)	≟	==	a ≟ b or a == b
Not equal (等しくない、ノットイコール)	≠	!=	a ≠ b or a != b
Less than (小なり)		<	a < b
Greater than (大なり)		>	a > b
Less or equal than (小なりイコール)	≤	<=	a ≤ b or a <= b
Greater or equal than (大なりイコール)	≥	>=	a ≥ b or a >= b

これらの演算子を使うと、2つの値が等しいかどうか、あるいは2つの値のどちらが大きいかを調べることができます。試しに「1は2より大きい(\(1>2\))」という命題をGeoGebraに入力してみましょう。その実行結果は以下のとおりです。

「1は2より大きい(\(1>2\))」は明らかに間違いですから、当然、結果は”false(偽)”になります。

等値判定演算

一般的なプログラミング言語と比較して、GeoGebraがユニークなのはさまざまなオブジェクトに対して等値判定演算を行うことができる点です。例えば、命題「aはbに等しい(a==b)」という論理演算があったとき、a、bは何らかの数であってもいいし、点や線、平面、円錐曲線であっても良いのです。また、CASモードの場合、a、bは関数であっても良いのです。

例えば、以下の2つの関数があるとします。

$$y=f(x)=\sin^2(x)$$

$$y=g(x)=\frac{1}{2}(1-\cos(x))$$

これらの関数に等値判定演算\(f(x)==g(x)\)を実行すると……

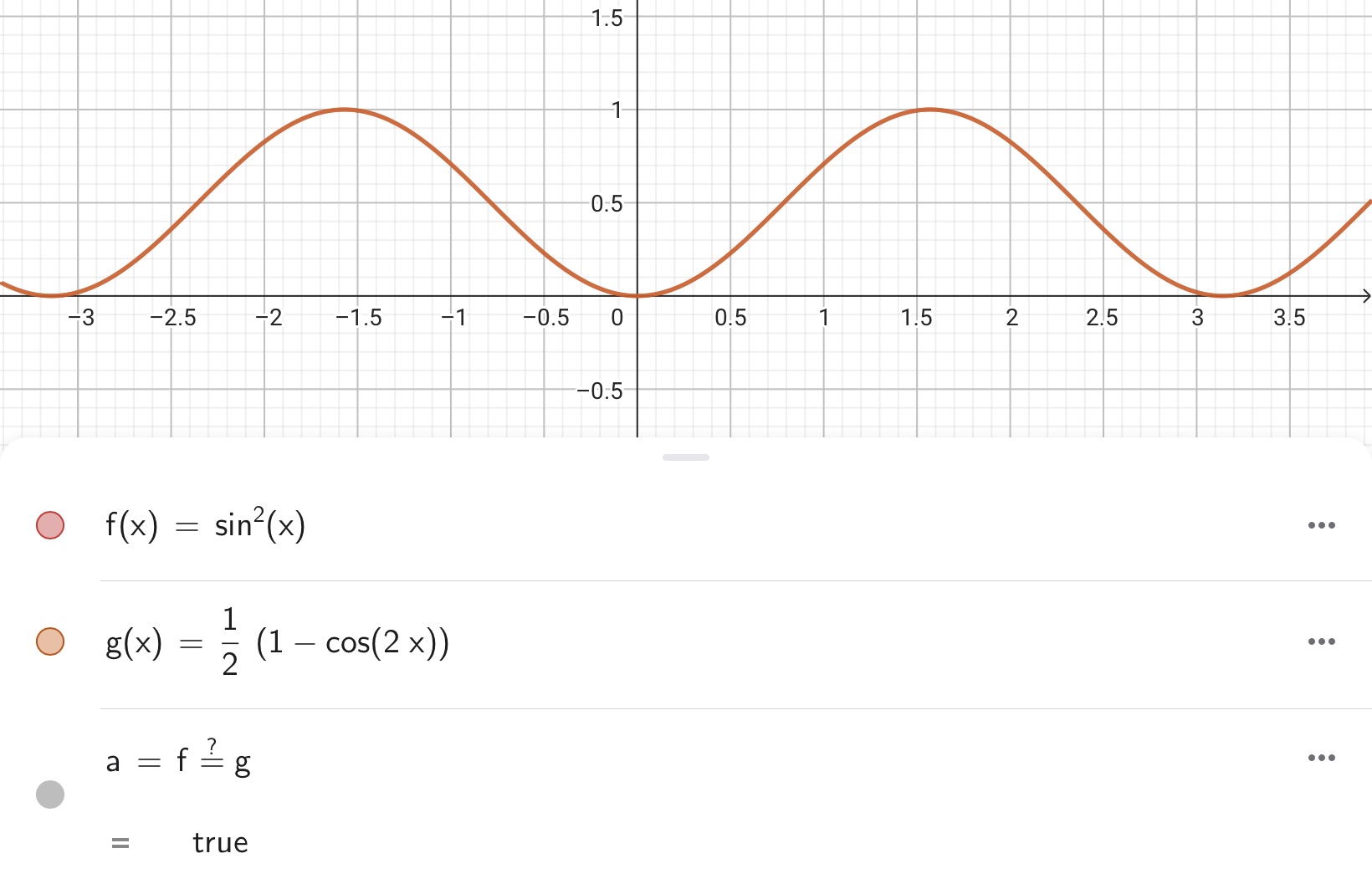
等値判定の演算結果は「true(真)」になりました。先ほどの2つの関数は「三角関数の2倍角の公式」として有名な数式です。

こうように、等値判定演算子を使うと2つのオブジェクト(数、点、線、平面、関数など)が等しいか、それとも等しくないかを簡単に判定することができます。数以外のオブジェクトにも等値演算を行うことができる点がとてもユニークです。

大小関係演算と不等式

GeoGebra公式サイト（ブール代数）の記述によると、大小関係演算子の入力は何らかの数だけです。点や線などを入力とすることはできません。ただし、大小関係演算子には「不等式」を記述するという機能もあります。大小関係演算子に関数を入力した場合、それは不等式として取り扱われます(この場合、「true(真)」や「false (偽)」は出力されません)。

すこし試してみましょう。例えば、大小関係演算子>の両辺に数値を入れてみます。例えば、先ほど説明したようにGeoGebraに\(1>2\)を入力してみましょう。この命題はもちろん「false (偽)」です。そのため、「false (偽)」と出力されます。

それでは、\(y>x\)と入力した場合はどうなるでしょうか？

この場合、GeoGebraは\(y>x\)を不等式として取り扱いますので、\(y>x\)のグラフを表示します。

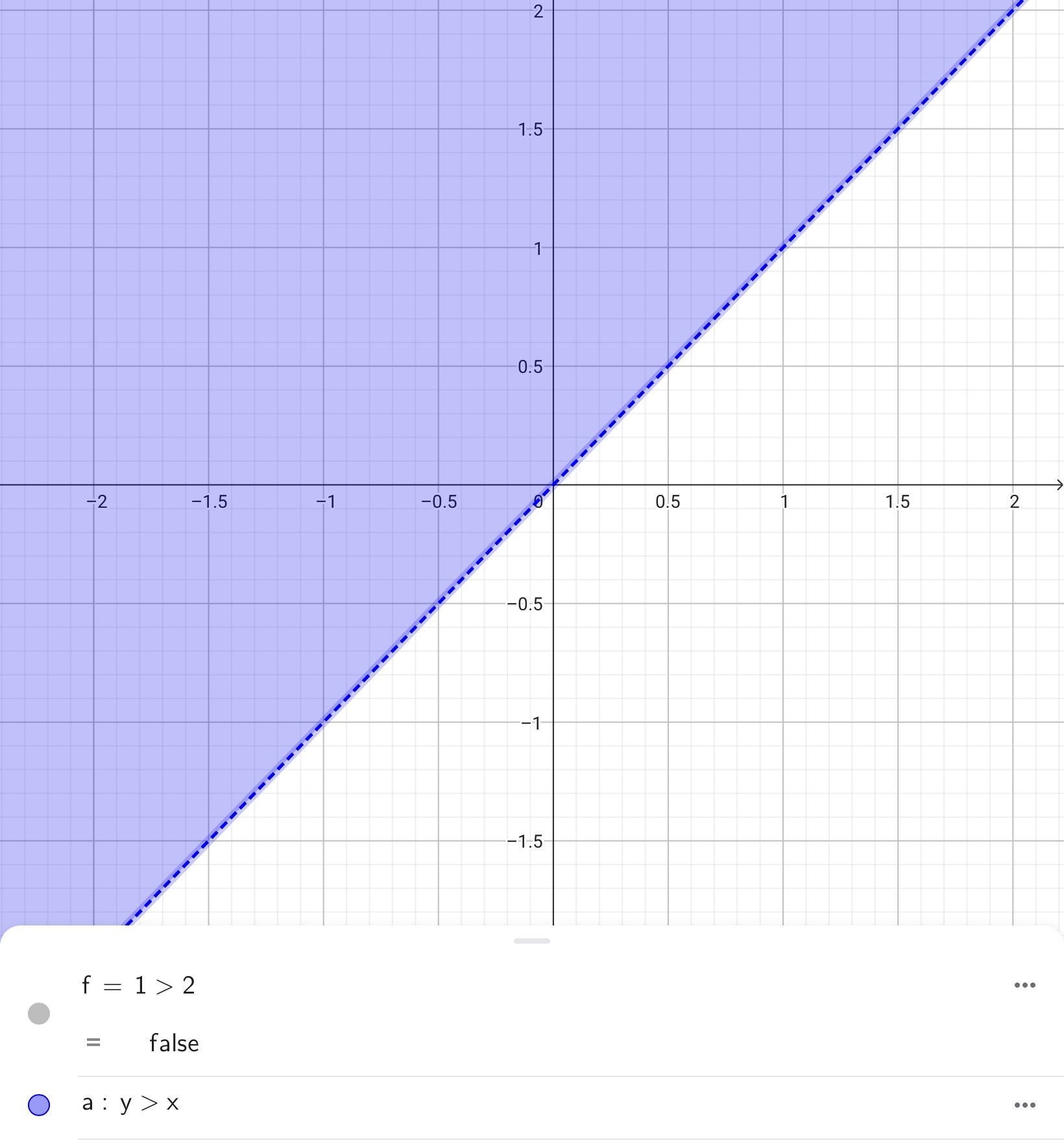
また、不等式と後述の論理演算子を組み合わせると、xy座標の一部を塗りつぶすことができます。例えば、こんな感じです。

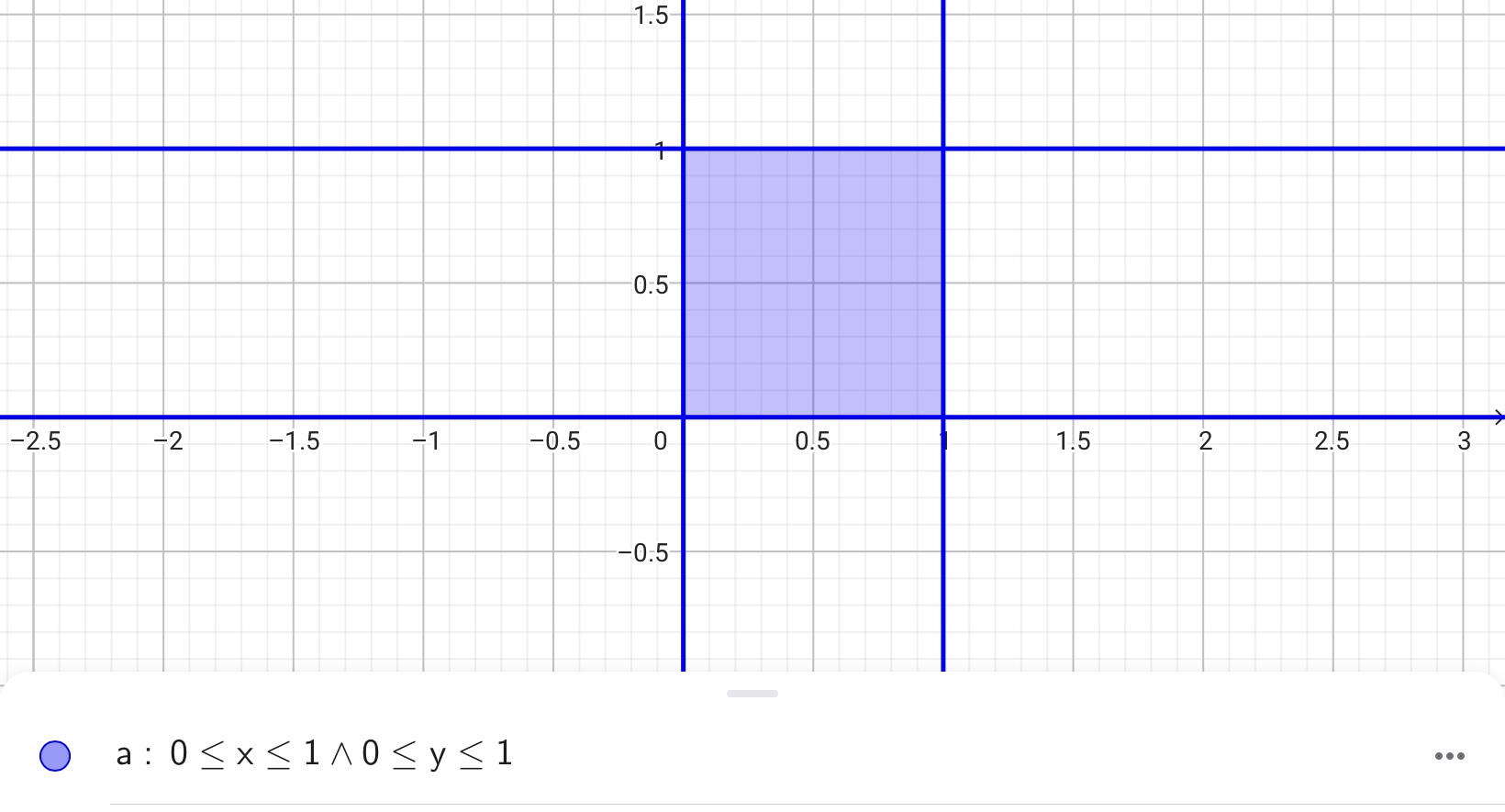
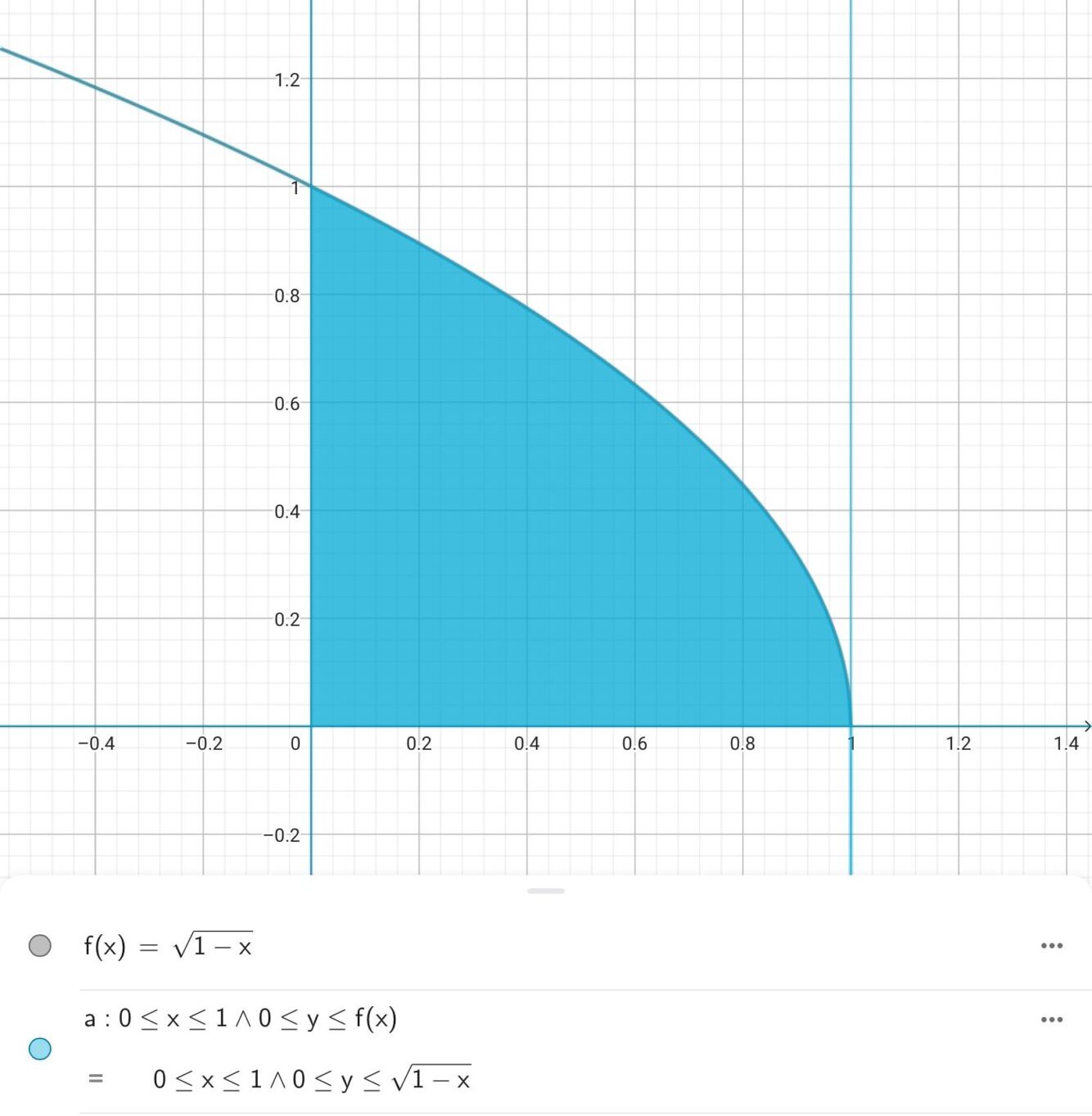
このようにGeoGebraを使うと複雑なグラフが簡単に描けるというだけでなく、xy座標の一部をきれいに塗りつぶすこともできます。

ブール代数の論理演算

GeoGebraはブール代数の論理演算として以下のコマンドをサポートしています。これらの論理演算コマンドを組み合わせることで、より複雑な論理演算を実行できます。

演算内容	入力バー	キーボード入力	例
And (かつ、論理積)	∧	&&	a ∧ b or a && b
Or (もしくは、論理和)	∨	||	a ∨ b or a || b
Not (否定)	¬	!	¬a or !a
Exclusive or (排他的論理和)		Alt+	a ⊕ b
Implication (含意)	→	->	a -> b

AND演算

2入力AND演算の真理値表は以下のとおりです。2入力AND演算は2つの入力がどちらも”true”の時だけ、”true”を出力します。

\(A\)	\(B\)	\(A \land B\)
”false”	”false”	”false”
”false”	”true”	”false”
”true”	”false”	”false”
”true”	”true”	”true”

OR演算

2入力OR演算の真理値表は以下のとおりです。2入力OR演算は2つの入力の少なくともどちらか一方が”true”の時に、”true”を出力します。

\(A\)	\(B\)	\(A \lor B\)
”false”	”false”	”false”
”false”	”true”	”true”
”true”	”false”	”true”
”true”	”true”	”true”

NOT演算

NOT演算の真理値表は以下のとおりです。NOT演算は入力が”true”の時は”false”を出力し、入力が”false”の時は”true”を出力します。

\(A\)	\(\overline{A}\)
”false”	”true”
”true”	”false”

排他的論理和

排他的論理和演算の真理値表は以下のとおりです。排他的論理和演算は2つの入力が一致しない時に”true”を出力します。

\(A\)	\(B\)	\(A ⊕ B\)
”false”	”false”	”false”
”false”	”true”	”true”
”true”	”false”	”true”
”true”	”true”	”false”

含意演算

含意演算の真理値表は以下のとおりです。含意演算\(A \rightarrow B\)は\(A\)が”true”の場合は\(B\)の値を出力します。一方、\(A\)が”false”の場合は、\(B\)の値によらず、常に”true”を出力します。

\(A\)	\(B\)	\(A \rightarrow B\)
”false”	”false”	”true”
”false”	”true”	”true”
”true”	”false”	”false”
”true”	”true”	”true”

なお、含意演算\(A \rightarrow B\)は\(\overline{A} \lor B \)と等価です。工学的な応用ではあまり出てこない演算子だと思いますが、覚えておくと便利かもしれません。

幾何学関連の論理演算

GeoGebraはもともと幾何学計算のために作られたコンピュータソフトウェアなので、幾何学的な論理演算として、以下の論理演算をサポートしています。これらの演算子を用いると、2つの直線が平行であるか否かや、垂直であるか否かを簡単に判定することができます。私の知る限り、他のプログラミング言語やコンピュータソフトウェアではこういった論理演算が存在するものはかなり珍しいと思います。

演算内容	入力バー	キーボード入力	例
Parallel(平行)	∥		a ∥ b
Perpendicular(垂直)	⊥		a ⊥ b

集合関連の論理演算

GeoGebraは集合関連の論理演算として、以下の演算をサポートしています。

演算内容	入力バー	キーボード入力	例
Belongs to(元として含む、属する)	∈		a ∈ list1
Subset (部分集合)	⊆		list1 ⊆ list2
Proper subset(真部分集合)	⊂		list1 ⊂ list2

なお、GeoGebraにおいて集合は「リスト機能」を用いて表現されます。リストを作るには中括弧｛｝を利用します。リストは入れ子構造にすることができ、使い方によっては3次元以上のテーブルを作ることもできます。リスト機能の詳しい使い方についてはいずれ別の記事で説明したいと思います。

まとめ

このページではGeoGebraの論理演算子について説明しました。GeoGebraというコンピュータソフトウェアを使いこなすためには、論理演算をしっかり学ぶ必要があります。論理演算は数学だけでなく、電子工学や情報工学でも役立つ概念なので、繰り返し勉強してしっかり理解しましょう。

このページは下記のサイトを参考にして作成されました。
GeoGebra公式サイト（ブール代数）

なお、GeoGebraの組み込み関数と演算子に関しては下記のページでも説明しています。こちらのページもお読みくださると幸いです。

GeoGebraの組み込み関数と演算子を学ぼう この記事は2024年3月現在のGeoGebra公式サイトをもとに作成しています。 この記事ではGeoGebraの組み込み関数と演...