前回の記事から、GeoGebraのオブジェクトについて説明しています。なお、この記事はGeoGebra公式サイト(オブジェクト関連ページ)をもとに作成されています。
前回は「オブジェクトとはそもそも何なのか?」、「オブジェクトにはどんな種類があるのか?」という点について説明しました。
前回の記事では、GeoGebraのオブジェクトには一般的なものと幾何学的なものの2種類があると述べました。これからの2つの記事では一般的なオブジェクトについて説明していきます。1つ目のこの記事では、数値、角度、複素数、ブーリアンについて説明します。
一般的なオブジェクト
数値
数値はもっとも基本的なオブジェクトの一つです。GeoGebraに数値を入力する場合、何も意識しなければ、GeoGebraは入力された数値を「10進数の実数」として取り扱います。なお、小数点にはピリオド(.)の記号を使います。
入力例
例えば、3.14という数字を入力してみましょう。
エンターキーを押すと……
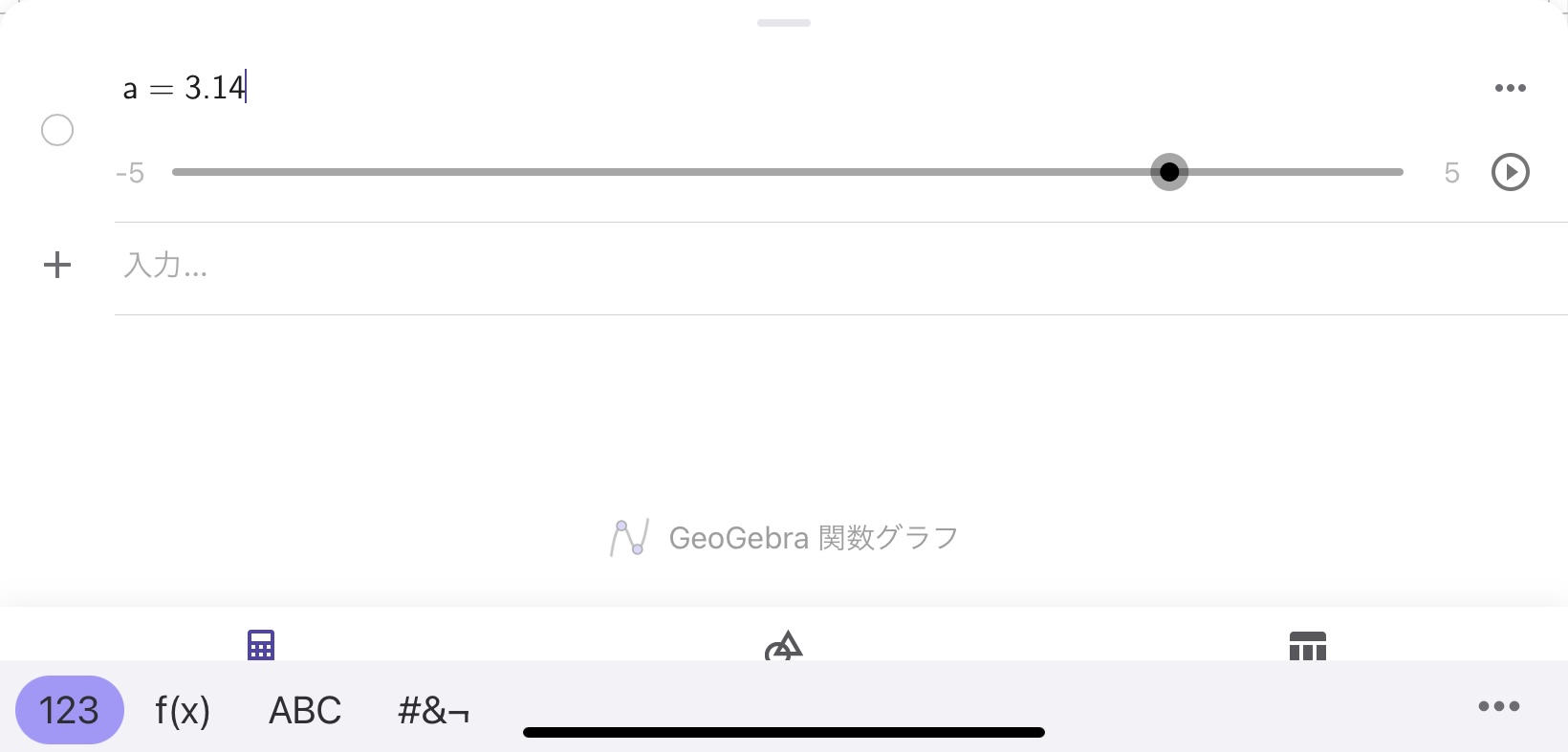
\(a=3.14\)と出力されるとともに、スライダーが表示されました(スライダーについては後で説明したいと思います)。
オブジェクトの命名
GeoGebraではたくさんのオブジェクトが取り扱われますが、複雑な数学計算を行うためにはどれがどのオブジェクトかを識別できるようにする必要があります。そのため、各オブジェクトには識別用の「名前」が付けられます。
オブジェクト名はユーザが指定しても良いですし、 GeoGebraに自動で名前を割り振らせても良いです。ユーザが名前を指定しない場合、GeoGebraは各オブジェクトに自動で名前を割り振ります。先ほどの例では、3.14という数値に\(a\)というオブジェクト名が自動的に割り振られました。
ユーザはある程度自由にオブジェクト名を決定することができますが、例外もあります。例えば、\(e\)と打ち込んでみましょう。
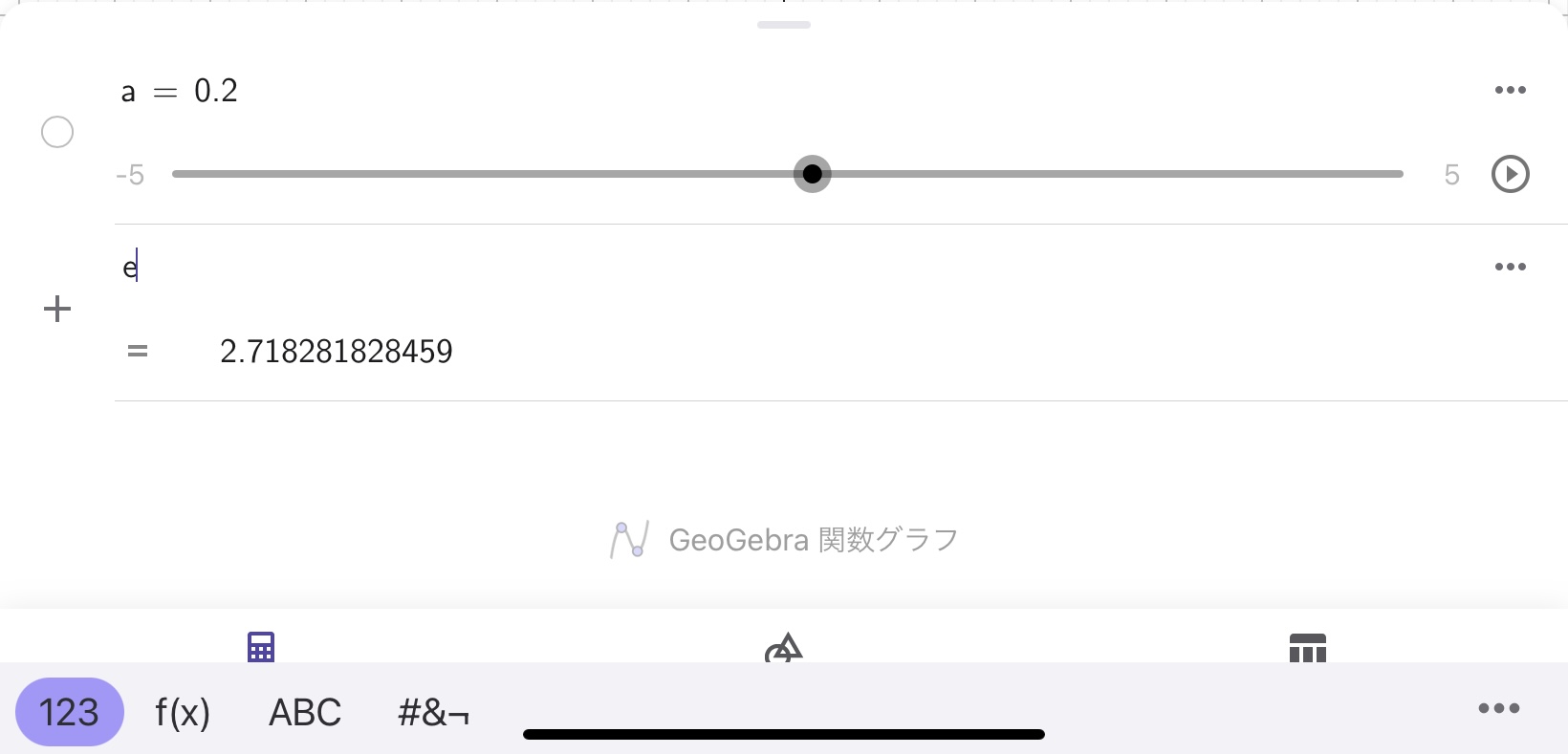
\(e\)と入力すると、エンターキーを押す前に=2.718……と表示されました。これはネイピア数と呼ばれる数字です。数学においてアルファベット小文字の\(e\)はネイピア数と定義されることが多いため、GeoGebraでもデフォルトでは\(e\)をネイピア数として定義しています。ただし、\(e\)という名称のオブジェクトを作ることはできます。例えば、\(e=6\)と打ち込んでみましょう。

\(e=6\)と打ち込んだところ、\(e\)という名称のオブジェクトができました。これ以後の計算では、\(e\)はネイピア数ではなく、先ほど作成されたオブジェクトとして扱われます。
ちなみに、GeoGebraにはオブジェクト名として使えない単語(予約語)もあります。予約語の代表例は\(\sin\)や\(\cos\)などです。予約語はいろいろありますが、「数学的に紛らわしいオブジェクト名はつけられない(また、つけるべきではない)」と覚えておけばいいでしょう。
数値の変更とスライダー
GeoGebraを使っていると、先ほど入力した数値を変更したくなることがあります。こういった場合、ユーザは数値を上書きすることができます。例えば、\(a=3.14\)と入力した後に、\(a=5\)と入力してみましょう。
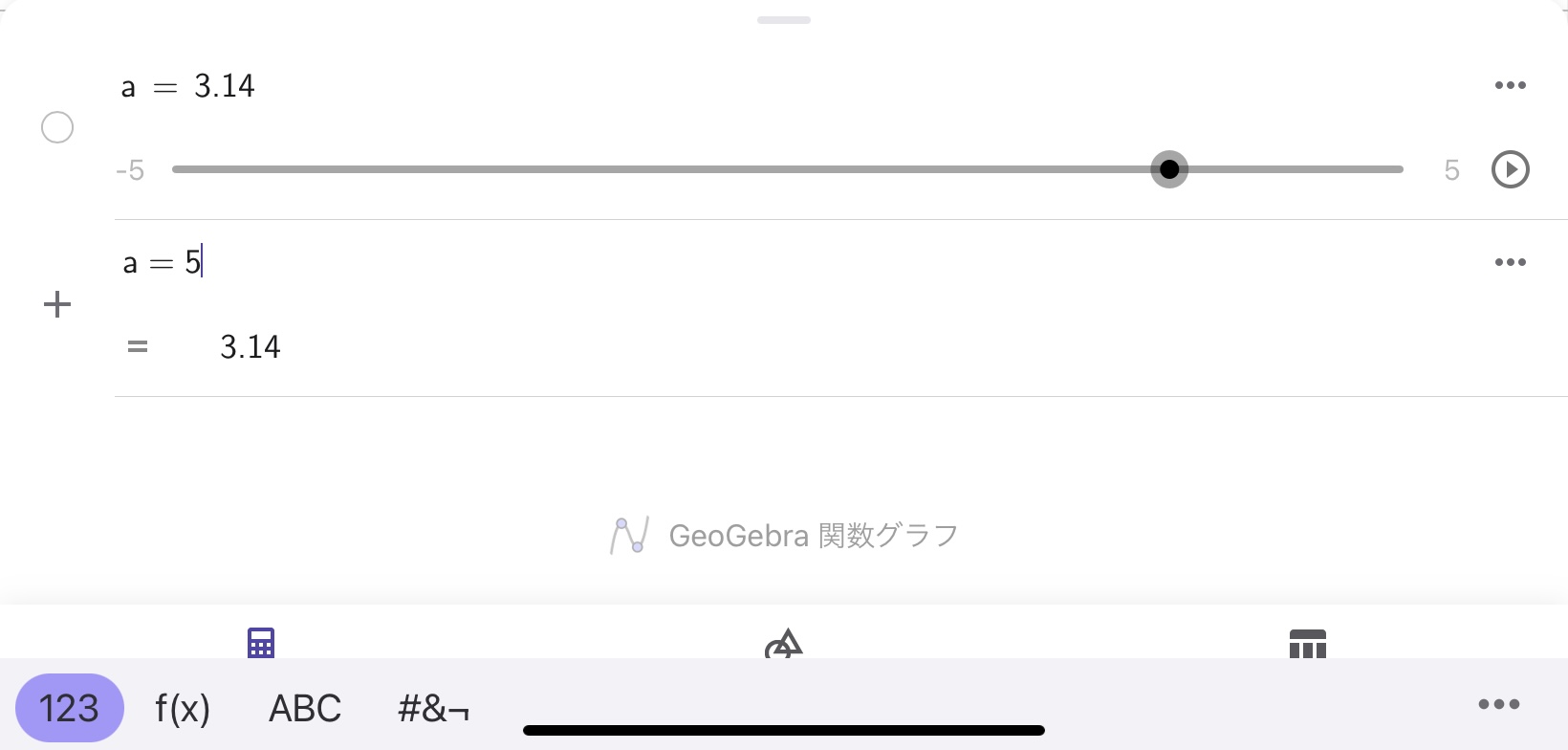
エンターキーを押すと、画面はこのように変わります。
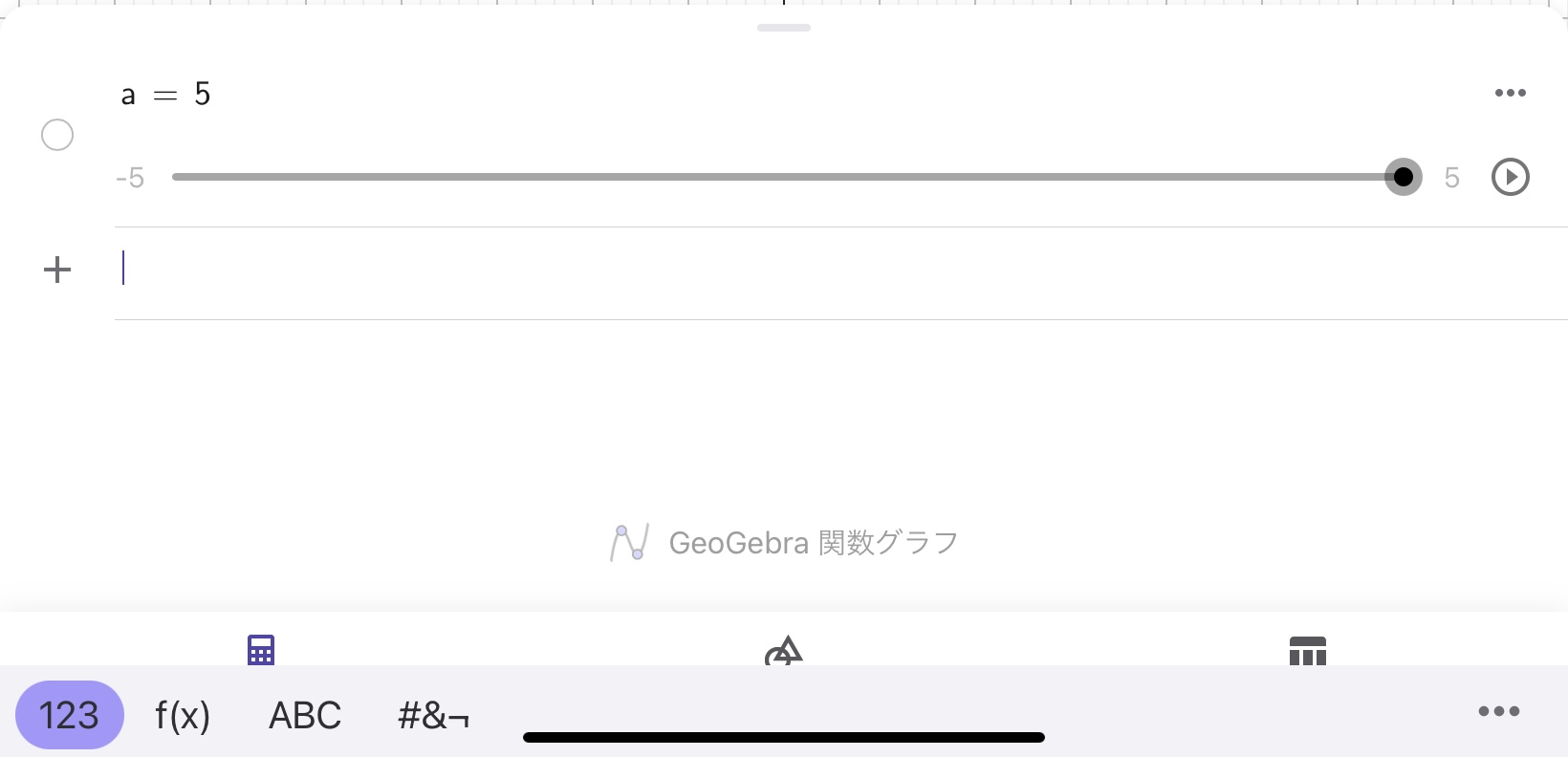
このように\(a\)という名称のオブジェクトは5という数字で上書きされました。\(a\)というオブジェクトの数値が上書きされたとき、その数値を使って演算される数式や図形があれば、それらは自動的に再計算されます。
ただ、いちいちキーボードを使って、数値の上書きをするのは面倒ですよね?そういった時はスライダー機能の出番です。

スライダーというのは、\(a\)というオブジェクトの下にある横棒のことです。スライダーのツマミを動かすと、数値の上書きをワンアクションで実行することができます。
さらに、スライダーは自動で動かすこともできます。例えば、\(y=a \cdot x\)と入力した後に、スライダーの再生ボタンを押してみてください。そうすると、グラフが自動的に変化していくはずです。
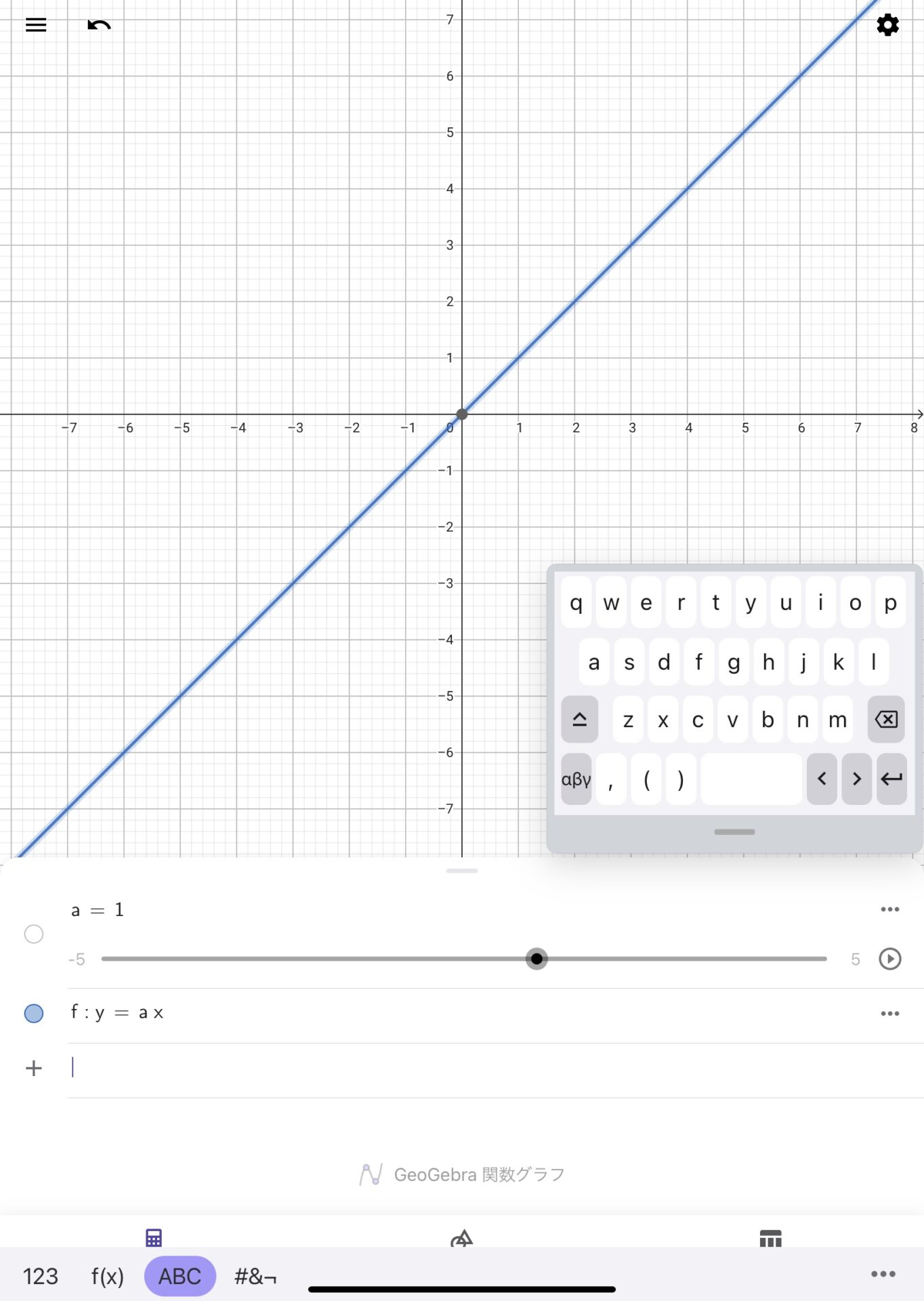
一次関数において、\(a\)は直線の傾きを意味します。スライダー機能で\(a\)を変更すると直線の傾きが変わることを確認してみてください。
角度
GeoGebraは幾何学図形の描画や三角関数の計算を行うのが得意です。これらの作業を行う時、角度を入力しなければならないことも多いです。GeoGebraで角度を入力する場合、度数法で入力することもできますし、弧度法で入力することもできます。
GeoGebraにおいて、角度を度数法で入力する場合、「°」の記号を数字の後ろに付けます。「°」の記号の付いていない角度は弧度法で表現された値であると、GeoGebraは解釈します。
大雑把に言うと、度数法と弧度法の違いは以下のとおりです。
- 度数法…直角の角度を90°と定義し、それを基準とした比率で角度を表す方法(1周すると360°になる)
- 弧度法…扇形の円弧の長さを使って角度を表す方法(1周すると\(2\pi\)になる)
弧度法は高校数学で習う内容なので、まだ習っていないと言う方のために、もう少し説明しておきましょう。以下の図は、弧度法の説明図です。
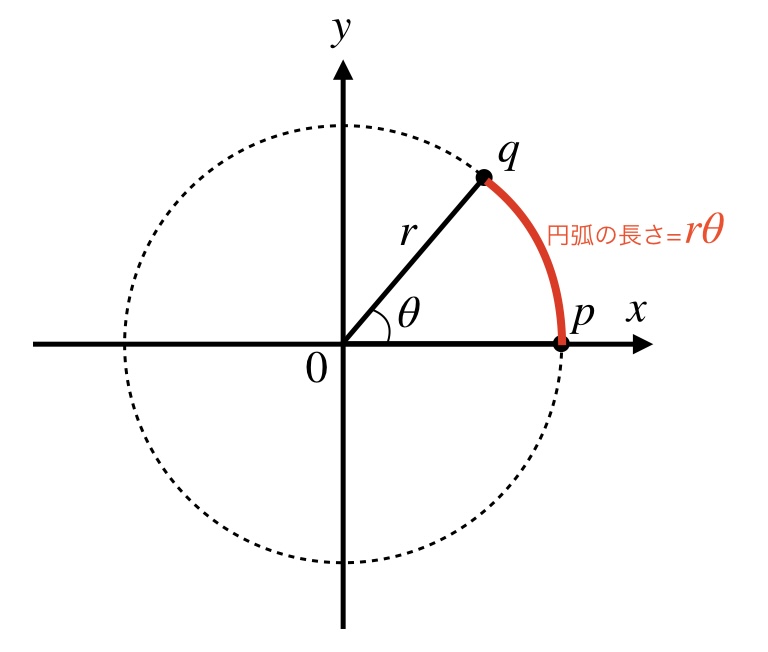
このxy平面には原点とx軸を基準として半径\(r\)、中心角度\(\theta\)の扇形が描かれています。この扇形の円弧の長さが半径\(r\)と中心角度\(\theta\)の掛け算(つまり、\(r \theta\))で表現できるように、角度というものを定義しようというのが弧度法の考え方です。
例えば、扇形の中心角度が360°の場合を考えてみましょう。これはいわゆる「普通の円」です。円の円周の長さは\(2\pi r\)ですから、弧度法で円の中心角度を表すと\(2\pi \)になります。このことから、度数法から弧度法への換算係数は\(\frac{2\pi}{360}\)になります。また、弧度法から度数法への換算係数は\(\frac{360}{2\pi}\)になります。
実はGeoGebraにおいて、「°」の記号は「数値に対して\(\frac{2\pi}{360}\)を乗じる」という意味なのです(GeoGebraはソフトウェア内部の計算をすべて弧度法で処理しています)。ですから、裏技的ですが、弧度法の角度を「°」で割ると度数法の角度が出てきます。実際にやってみましょう。

\(2\pi \)に\(\frac{360}{2\pi}\)を乗じたので\(360\)と出力されました。
ちなみに、逆三角関数を演算するときなどには、演算結果を度数法で出力してもらいたいケースがあります。GeoGebraでは、逆三角関数の結果を度数法で出力することもできます。このことについてはほかの記事で触れたので、詳しく知りたい方はそちらをご覧ください。
複素数
数学では、実数\(a\)、\(b\)と虚数単位\(i=sqrt{-1}\)によって\(z=a+bi\)と表すことができる数のことを複素数と呼びます。GeoGebraでは複素数の計算を行うこともできます。
複素数の計算を行う方法は簡単です。虚数単位ίを入力バーのシンボルボックスから選択するか、キーボードのALTキーを押しながらiを入力すれば良いのです。また、CASモードではiという名称のオブジェクトをユーザが作成しない限り、アルファベットの小文字のiが自動的に虚数単位として解釈されます。
GeoGebraは複素数の四則演算(加減乗除)が可能です。また、GeoGebraは以下のリストに記載されたコマンドを利用して、各種の複素演算を実行することが可能です。
| 演算/関数 | 入力方法 |
| ί (虚数単位) | Alt + i |
| 共役 | conjugate( ) or Reflect[ w ,xAxis] |
| 偏角 | arg( ) or Angle[w] |
| 絶対値 | abs( ) or Length[w] |
| 実数部分 | real( ) or x(w) |
| 虚数部分 | imaginary( ) or y(w) |
Note: arg( )は出力を-180°〜180°の範囲で返すのに対して、Angle[ ]は出力を0°〜 360°の範囲で返します。
Note: GeoGebraを使っていると、あるオブジェクトが複素数かどうか、判定したい場合があります(※一部のコマンドは実数オブジェクトに対して働かないため)。あるオブジェクトが複素数かどうかを判定するにはimaginary(a)≠0と入力するのが良いと思います。
なお、複素数はオイラーの公式を利用して、指数関数の形(いわゆる極座標形式)で表現することも可能です。半径\(r\)と偏角\(\theta\)を用いると、指数関数の形で以下のように複素数を表現することができます。
$$r e^{i\theta}=r \cos\theta+i r \sin\theta$$
GeoGebraでは、exp()コマンドやe^()(ネイピア数のべき乗)を利用して、指数関数の形で複素数を入力することができます。
GeoGebraには他にも複素数関連のコマンドがあります。それに関してはいずれご紹介したいと思います。
ブーリアン
他の多くのプログラミング言語と同様、GeoGebraではブール型の変数(Boolean、ブーリアン)を扱うことができます。ブール型変数というのは論理演算を取り扱うための専用の変数型で、「true(真)」と「false (偽)」の2値を取り扱います。
入力された命題が成り立つときブール型変数の出力は「true(真)」になり、成り立たないときブール型変数の出力は「false (偽)」になります。
ブール型変数については下記の記事で詳しくご紹介しましたので、詳しくはそちらをご覧ください。
まとめ
この記事ではGeoGebraの一般的なオブジェクトとして、数値、角度、複素数、ブーリアンについてについて説明しました。オブジェクトについて学ぶことで、GeoGebraの使い方に対する理解を深めていくことができます。次回もオブジェクトについて解説していきますので、ぜひお読みください。









[…] GeoGebraのオブジェクトを学ぼう(2) 前回の記事から、GeoGebraのオブジェクトについて説明しています。なお、この記事はGeoGebra公式サイト(オブジェクト関連ペー… […]