いくつか前の記事から、GeoGebraのオブジェクトについて説明しています。なお、この記事はGeoGebra公式サイト(オブジェクト関連ページ)をもとに作成されています。
GeoGebraのオブジェクトには一般的なものと幾何学的なものの2種類があります。今回の記事は、前回の記事に引き続き、幾何学的なオブジェクトについて説明していきます。
関数の描画
基本的な使い方
GeoGebraは様々な関数を描画できます。下記のページはGeoGebraの組み込み関数をまとめたものですが、そこにまとめたコマンドだけでも、三角関数や指数関数、対数関数、双曲線関数、特殊関数などを描画することができます。
GeoGebraは数式を入力するだけで、複雑な関数のグラフを描画できるのでとても便利です。一例として、名も無き関数の描画例を示します。
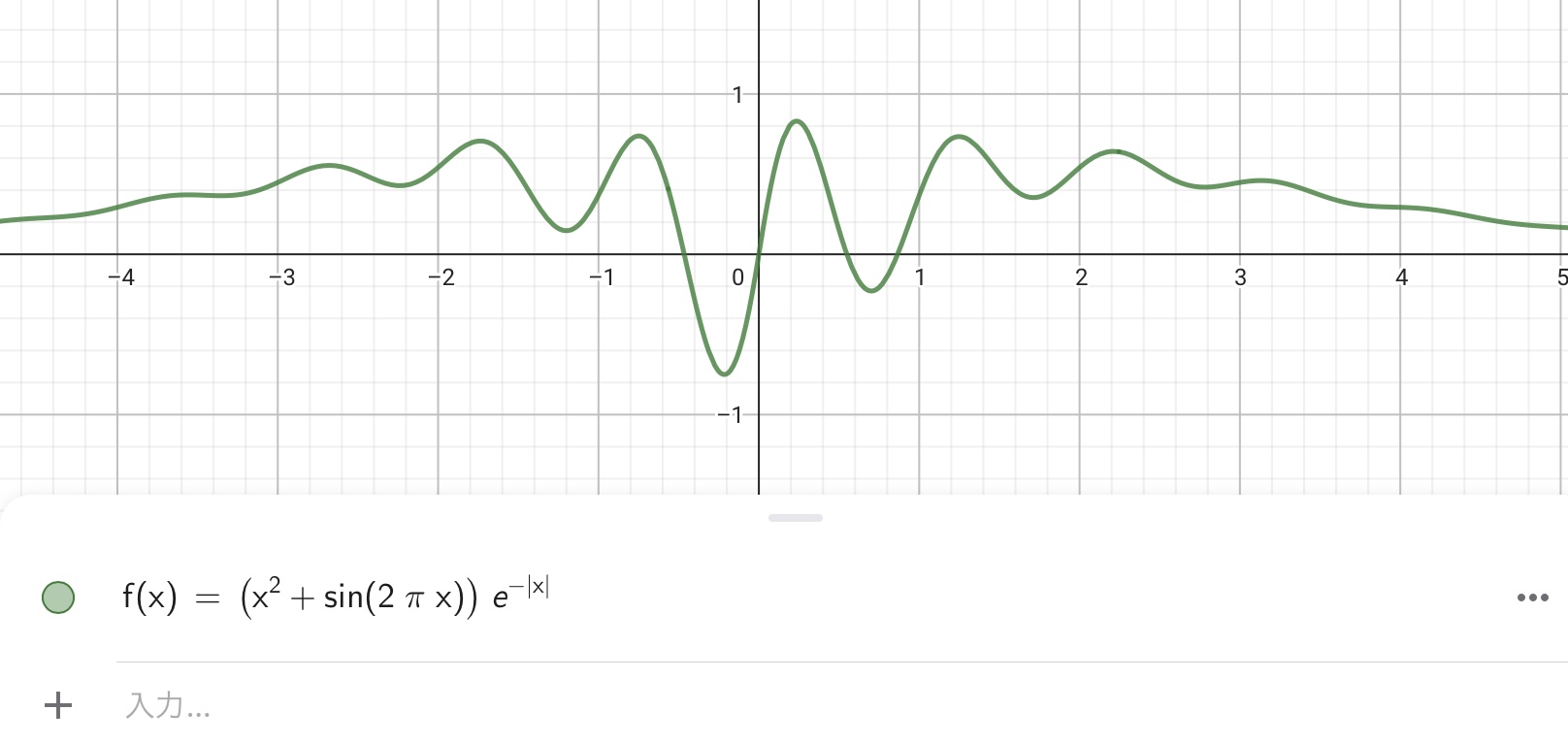
理工系の参考書や学術書を読んでいると、とても複雑な数式が出てくることがよくあります。そういう時はGeoGebraでグラフを描いてみると理解が深まるかもしれませんね。
関数を用いた演算
GeoGebraでは、関数に対して様々な演算を行うことができます。以下の画像を見てください。
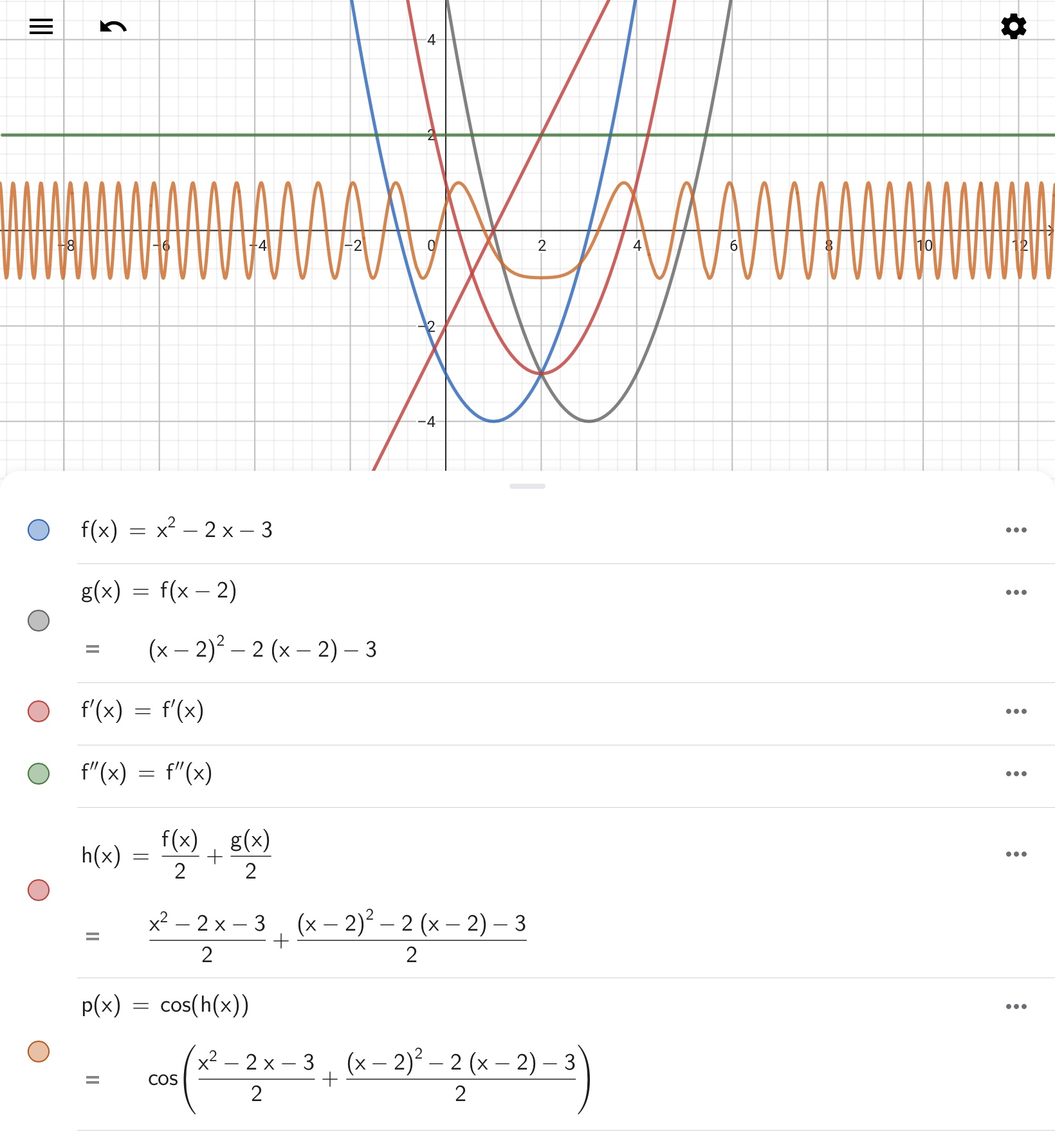
この図では、二次関数\(f(x)=x^2-2x-3\)に対して様々な演算を実行しています。適当に作った計算例なので理工学的な意味はほとんどないのですが、上から順に見ていきましょう。
関数\(g(x)\)は関数\(f(x)\)を右方向(x軸方向)に水平移動させたものです。関数を右方向に水平移動させるには、例えば、\(g(x)=f(x-2)\)というように入力すれば良いです。灰色の線が青い線に対して右方向に水平移動していることを確認してください。
\(f(x)\)の導関数(すなわち\(\frac{\mathrm{d}}{\mathrm{d}x}f(x)=f’(x)\))をGeoGebraに計算させるには’(ダッシュ記号)を用いてf’(x)と入力すれば良いです(Derivativeコマンドを使う方法もあります)。2階微分を計算したい場合はf’’(x)と入力してください。この例では一階微分は一次関数に、2階微分は定数になります。図中の赤い直線と緑の直線がそれぞれ一次関数と定数であることを確認してください。
関数\(h(x)\)は関数\(f(x)\)と関数\(g(x)\)の平均値を計算したものです。GeoGebraでは関数に対して四則演算を実行し、新たな関数を作成することができます。
関数\(p(x)\)は関数\(h(x)\)を入力とする三角関数を計算したものです。これも関数オブジェクトから新たな関数オブジェクトを作成した一例でしょう。
このようにGeoGebraでは、関数オブジェクトに対して様々な演算を実行することができます。実行した演算によって新しく生成された関数オブジェクトはもちろん自動的にグラフ化されます。そのため、GeoGebraを使うとたくさんのグラフを簡単に作れるのです。そして、たくさんのグラフを描いてみることによって、理工学系の科目を効率的に学ぶことが可能となるのです。
関数の範囲を制限する
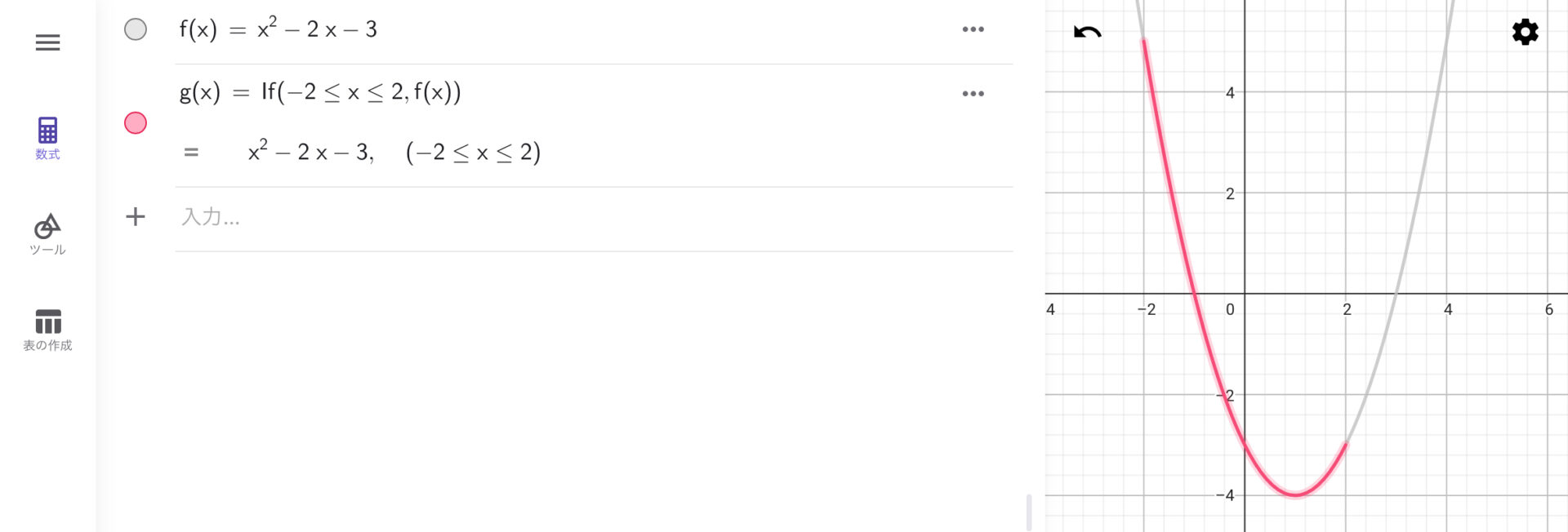
グラフを描くときに入力値の範囲を制限したくなる時があります。そういった場合はIf()コマンドかFunctionコマンドを利用します。以下の例は先ほどの二次関数のグラフの範囲を制限したものです。ピンクの曲線が\( -2 \leq x \leq 2\)の範囲だけ描画されていることを確認してください。
媒介変数によるグラフの描画
前回までの記事でも触れましたが、GeoGebraでは媒介変数を用いてグラフを描画することができます。媒介変数を用いて直線や円を描画する方法については前回までの記事ですでに述べましたので、今回の記事では応用としてインボリュート曲線を描いてみます。
インボリュート曲線というのは下記の渦巻き状の曲線のことです。ぐるぐる回りながら半径が大きくなる曲線ですね。機械工学の分野では、インボリュート曲線は歯車の設計などに用いられるそうです。
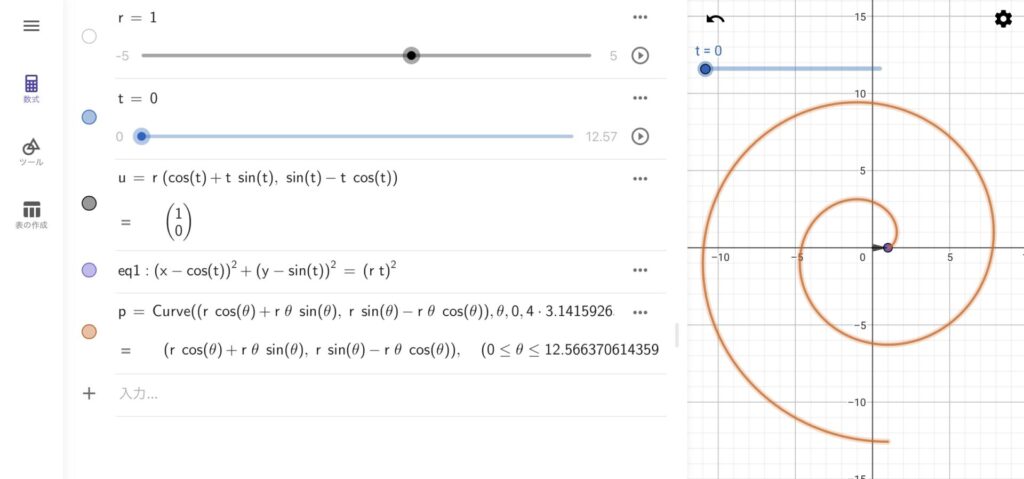
インボリュート曲線は数学的には下記の数式で表されます。
$$x=r \cos(\theta) + \theta \sin(\theta), y=r \sin(\theta) – \theta \cos(\theta)$$
ただし、\(r\)は定数、\(\theta\)は角度です。上記の数式は\(\theta\)を媒介変数とする数式になっていますね。この数式をGeoGebraに入力すると、グラフが自動的に描画されます。ただし、ここではCurve( )というコマンドを使って、媒介変数が\(\theta\)という文字で表されることをGeoGebraに伝えています。また、\( 0 \leq \theta\ \leq 4 \pi\)の範囲でグラフを描くように命令しています。具体的には、Curve(xに関する式,yに関する式,媒介変数,媒介変数の初期値,媒介変数の最終値)というコマンドを入力しています。各コマンドには複数の入力方法があるのが一般的なので、詳しい使用方法はマニュアルを参照してください。
媒介変数を使いこなすと複雑なグラフを簡単な数式で表現できることがあります。しかし、通常の表計算ソフトでその数式をグラフ化するのは大変です。GeoGebraのメリットの一つは媒介変数を用いたグラフを簡単に描画できることです。ぜひ、この機能を使いこなせるようになってくださいね。
不等式の描画
ここまで説明してきた幾何オブジェクトは基本的に等式によって記述されるものでしたが、GeoGebraは不等式を取り扱うこともできます。一般的な表計算ソフトウェアや科学計算用ソフトウェアは不等式グラフの描画が苦手なものが多いので、不等式の取り扱いが得意なことはGeoGebraの優れた特長のひとつです。以下にいくつか例を示します。
基本的な描画方法
下図は\(x^2 \geq x+1\)という不等式を満たす範囲を描画したものです。GeoGebraは不等式が入力されると、その不等式を自動的に解いて、不等式が満たす範囲をグラフに描画します。下図では、この不等式を満たす範囲が青色で塗りつぶされています。この不等式の解は\(x \geq \frac{1+\sqrt{5}}{2}\simeq 1.62,x \leq \frac{1-\sqrt{5}}{2}\simeq -0.62\)ですが、この範囲が青く塗りつぶされていることを確認してください。
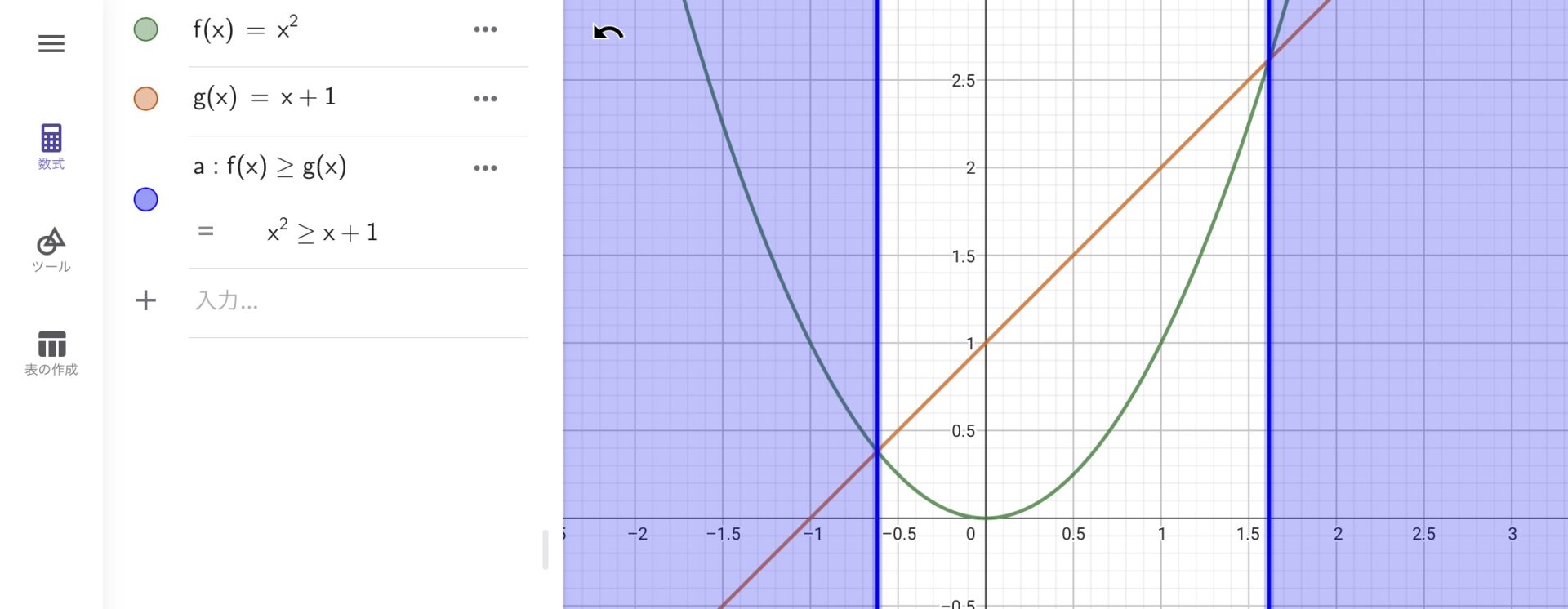
先ほどの例はxに関する二次不等式で、不等式を満たす範囲と満たさない範囲の境目が直線になりました。これは比較的、簡単な不等式です。
GeoGebraはこれよりも複雑な不等式を入力した場合でも、不等式を満たす範囲を図示できます。以下の3つの図は不等式を満たす範囲と満たさない範囲の境目が曲線的になるような事例です。
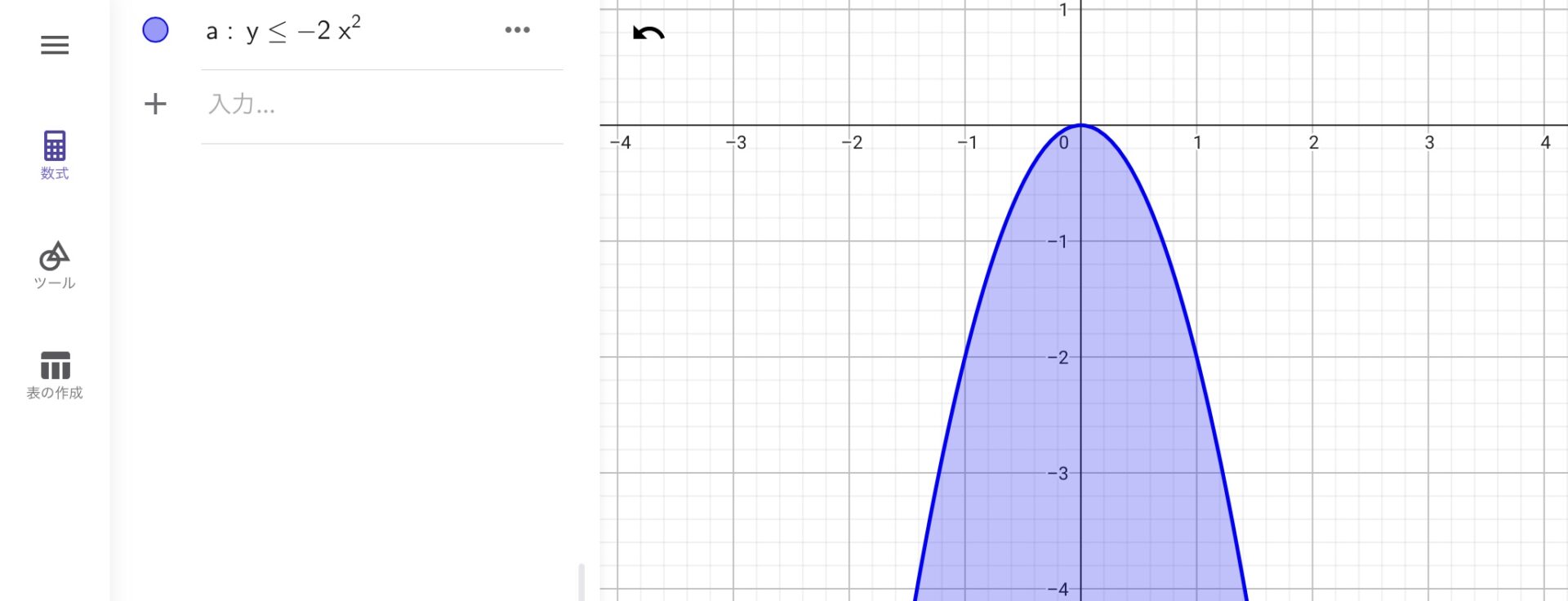
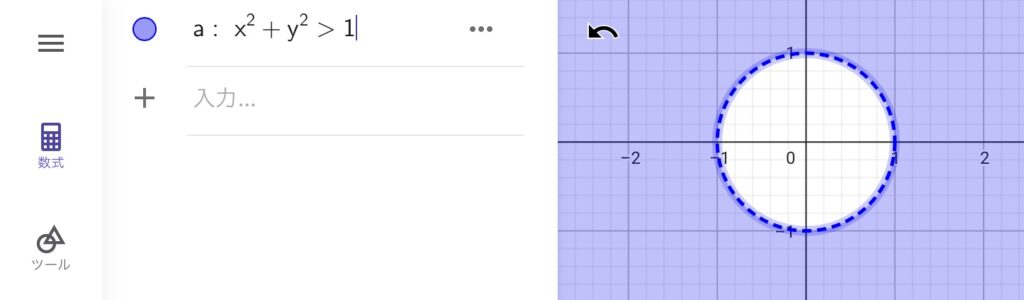
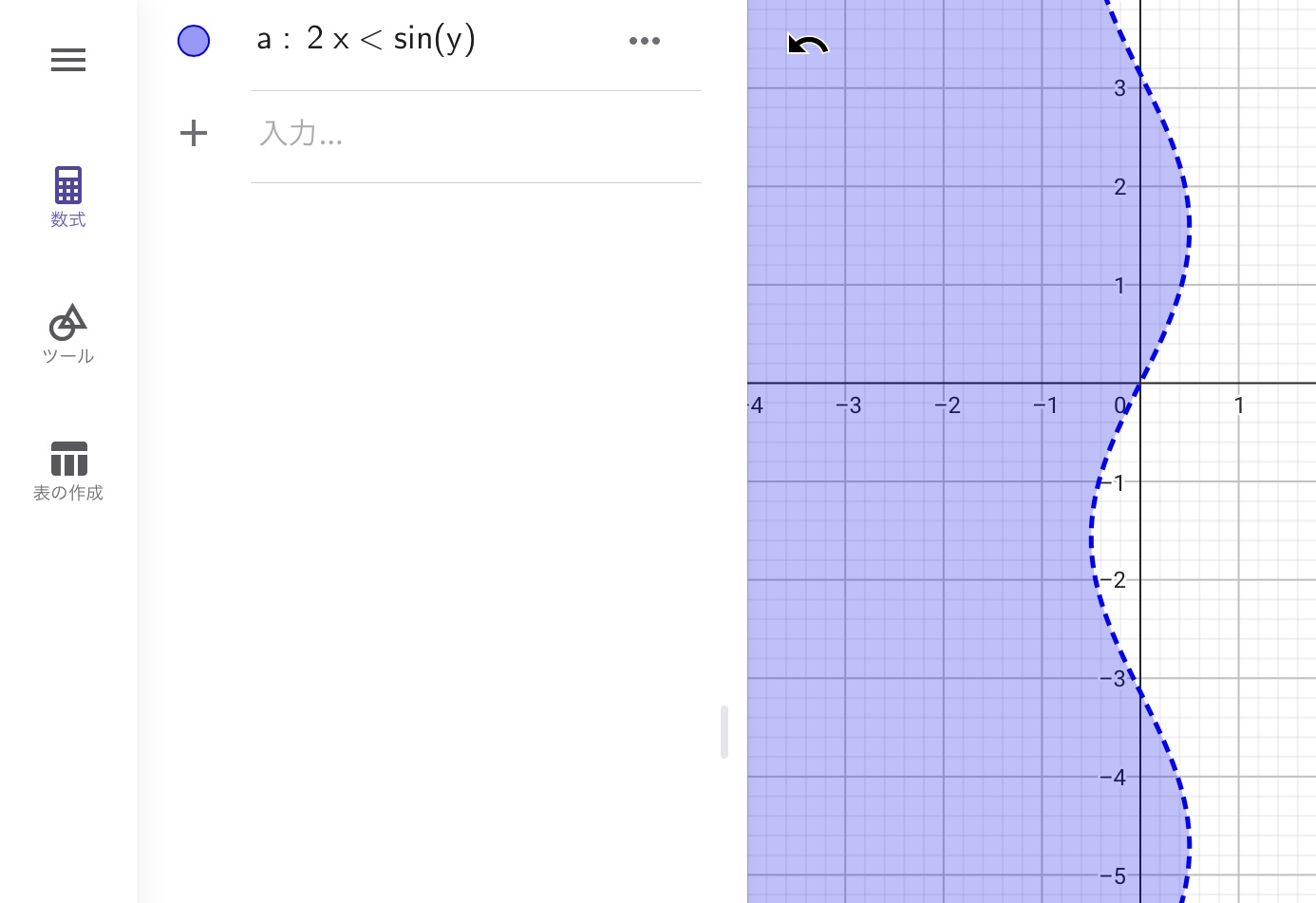
これらの図を見てわかる通り、GeoGebraのようなグラフ計算ソフトは不等式の計算が得意です。
点が不等式を満たすか判定する
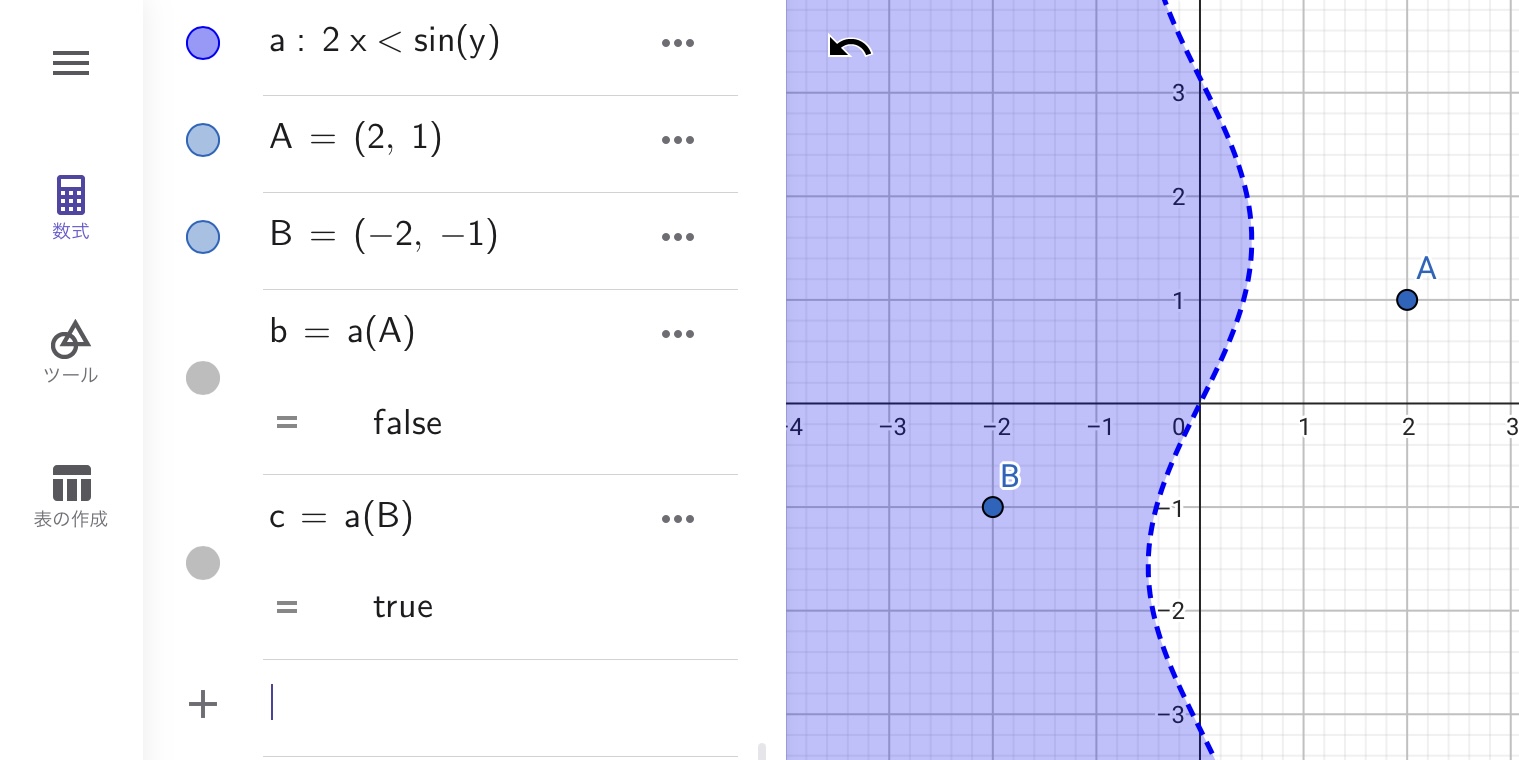
GeoGebraは任意の点オブジェクトが不等式を満たすか否かを判定する演算を備えています。不等式のオブジェクト名(点)と入力すると、その点が不等式を満たすか否かが判定され、満たす場合は”true(真)”、満たさない場合は”false(偽)”が出力されます。
以下の図を見てください。この図では先ほどの不等式と適当にプロットした点A、Bが描画されています。ここでは不等式のオブジェクトが小文字のaですので、点A、Bが不等式を満たすか否かを判定するにはa(A)やa(B)と入力します。図から点Aは不等式の範囲外であり、点Bが範囲内であることはすぐにわかりますが、この判定演算の結果が正しく出力されていることを確認してください。
AND演算とOR演算の活用
GeoGebraでは、AND演算(論理積演算)とOR演算(論理和演算)を利用することで、より複雑な不等式オブジェクトを表現できます。いくつか例を見てみましょう。
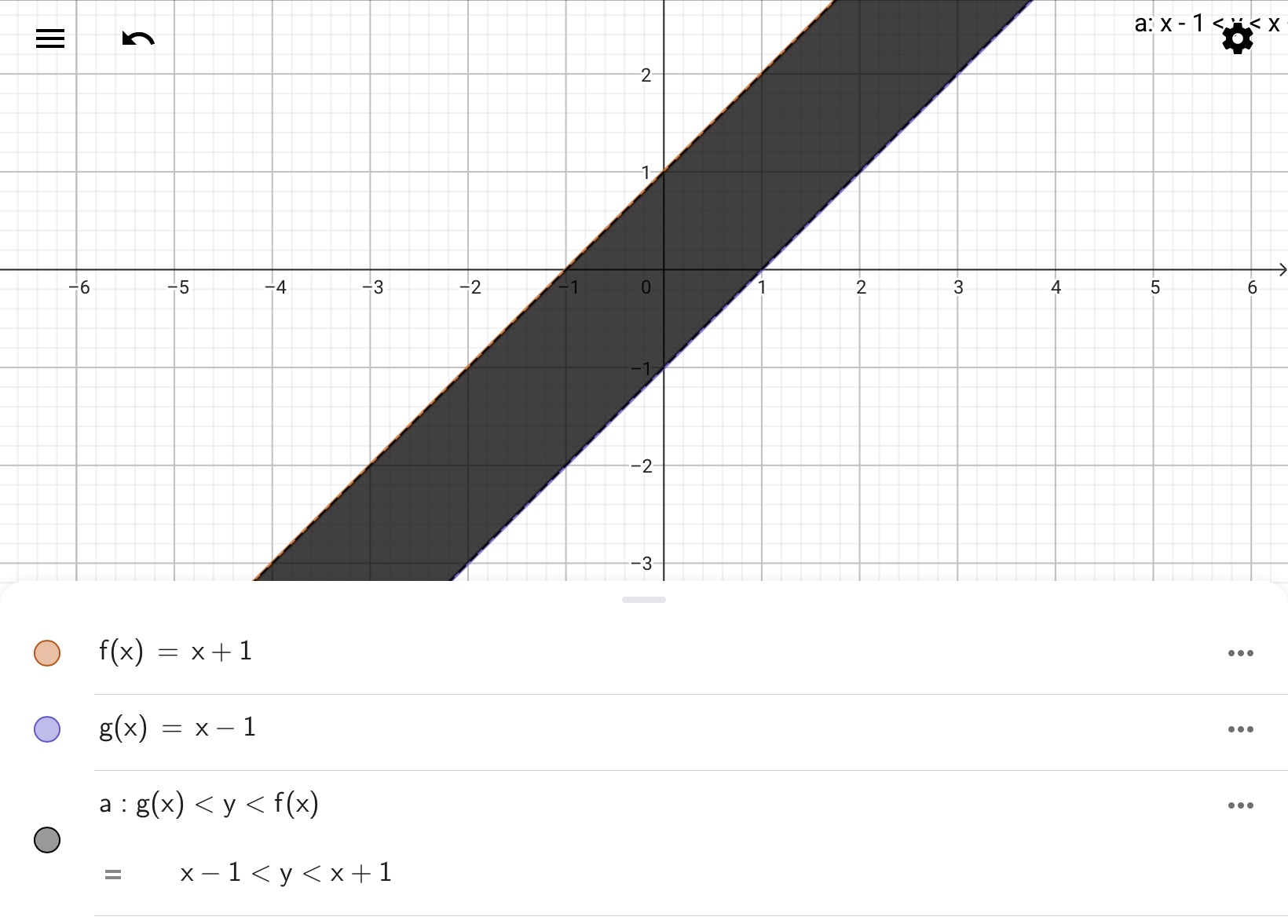
以下の例では、変数\(y\)と関数\(f(x),g(x)\)に関する不等式オブジェクトを描画しています。ここで、\(f(x),g(x)\)は平行な直線としています。さて、\(y<f(x)\)かつ\(g(x)<y\)を満たす範囲を描画してみましょう。「かつ」というのは、AND演算(論理積演算)に相当します。この2つの不等式は\(g(x)<y<f(x)\)にまとめることができます(※これはある種のAND演算です)から、これをGeoGebraに入力してみます。すると、\(g(x)<y<f(x)\)を満たす範囲が塗りつぶされます(下図では黒く塗りつぶされています)。
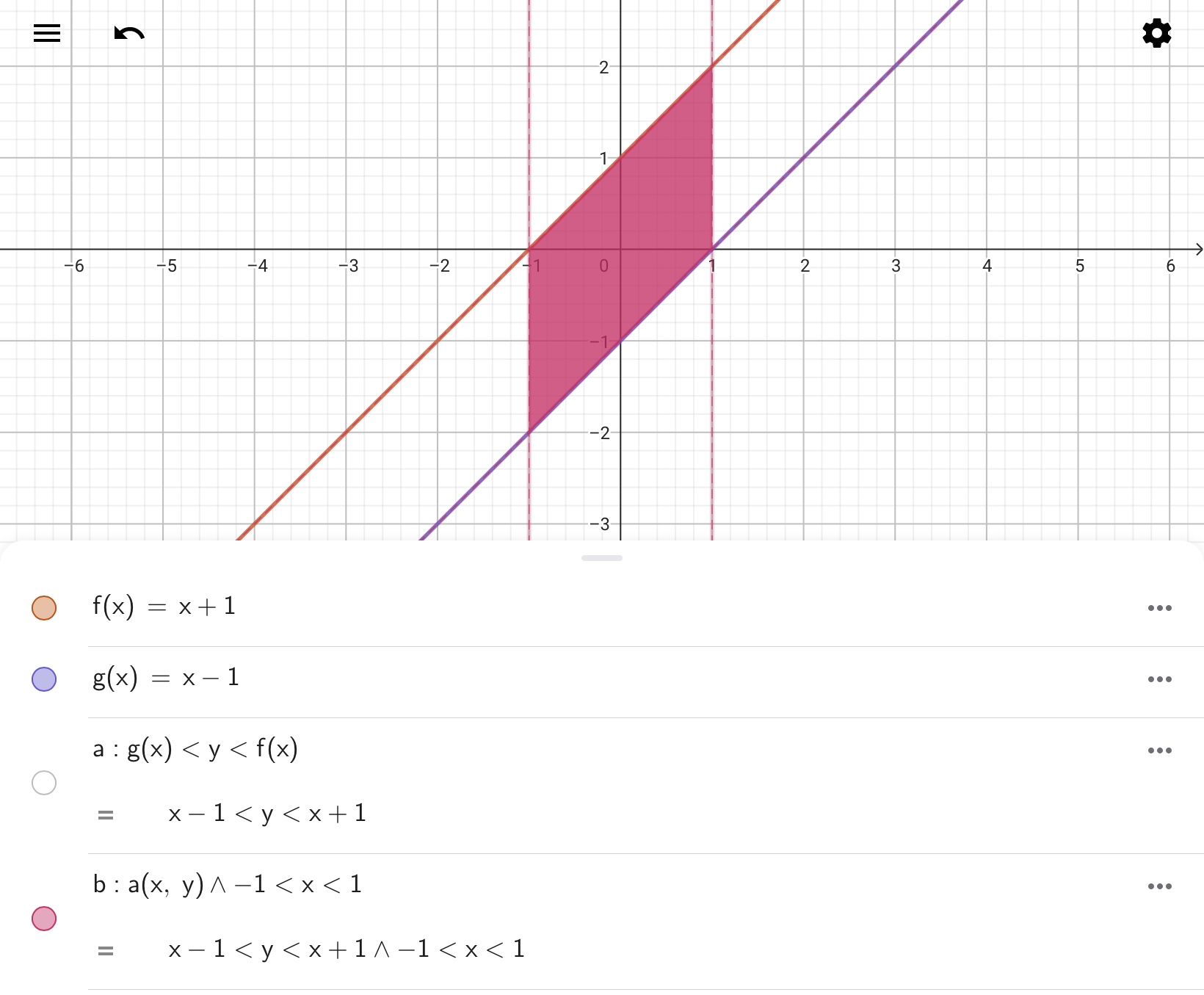
ほかの不等式をさらにAND条件で追加することもできます。以下の図を見てください。ここでは、\(g(x)<y<f(x)\)かつ\(-1<x<1\)の範囲を描画しています。GeoGebraでは、AND演算(論理積演算)の演算子として∧、もしくは&&が利用できます。このようにAND演算を使うと複数の不等式を同時に満たす範囲を描画できます。
次はOR演算を使ってみましょう。例えば以下の図に示すような領域a、bがあるとします。
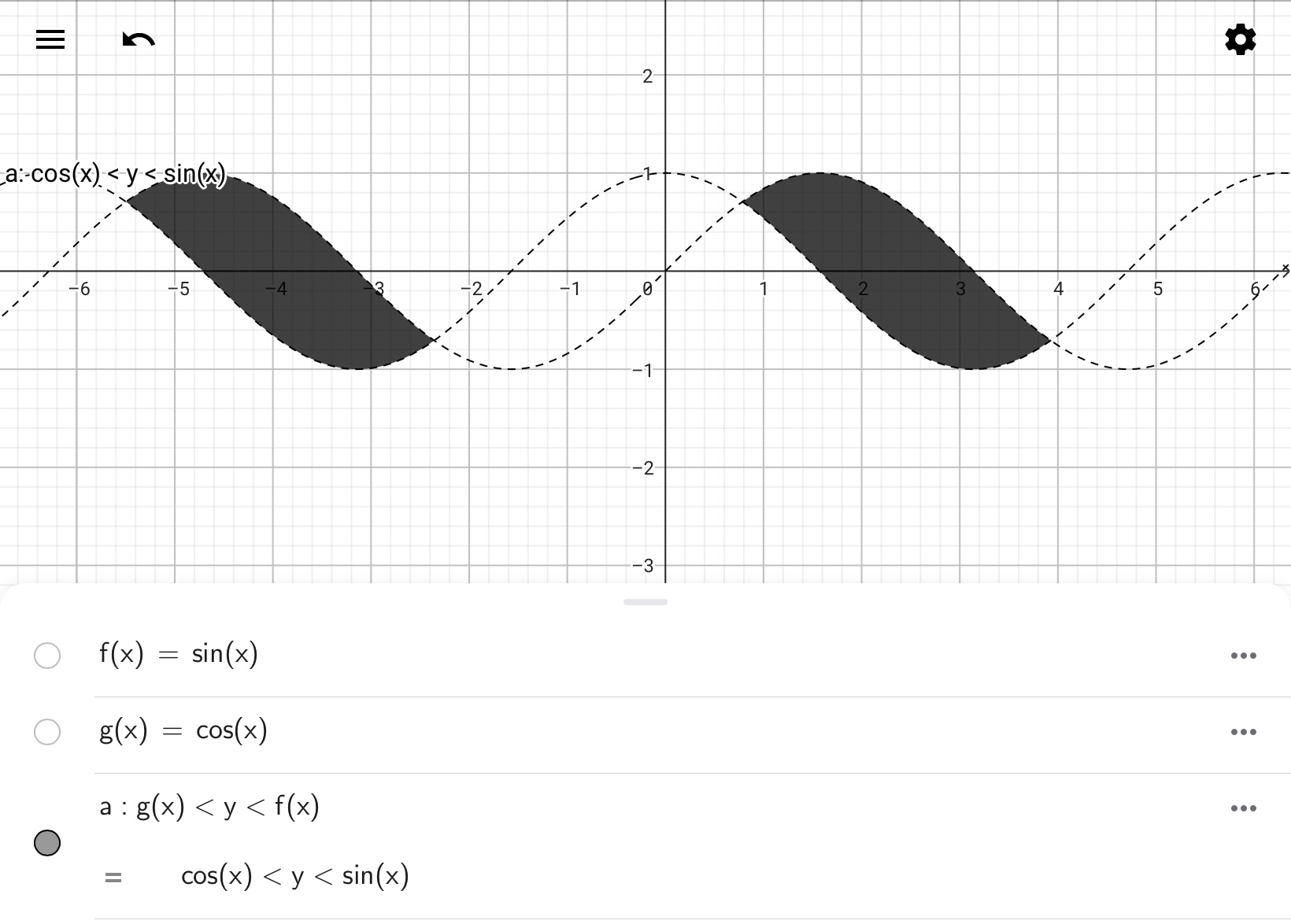
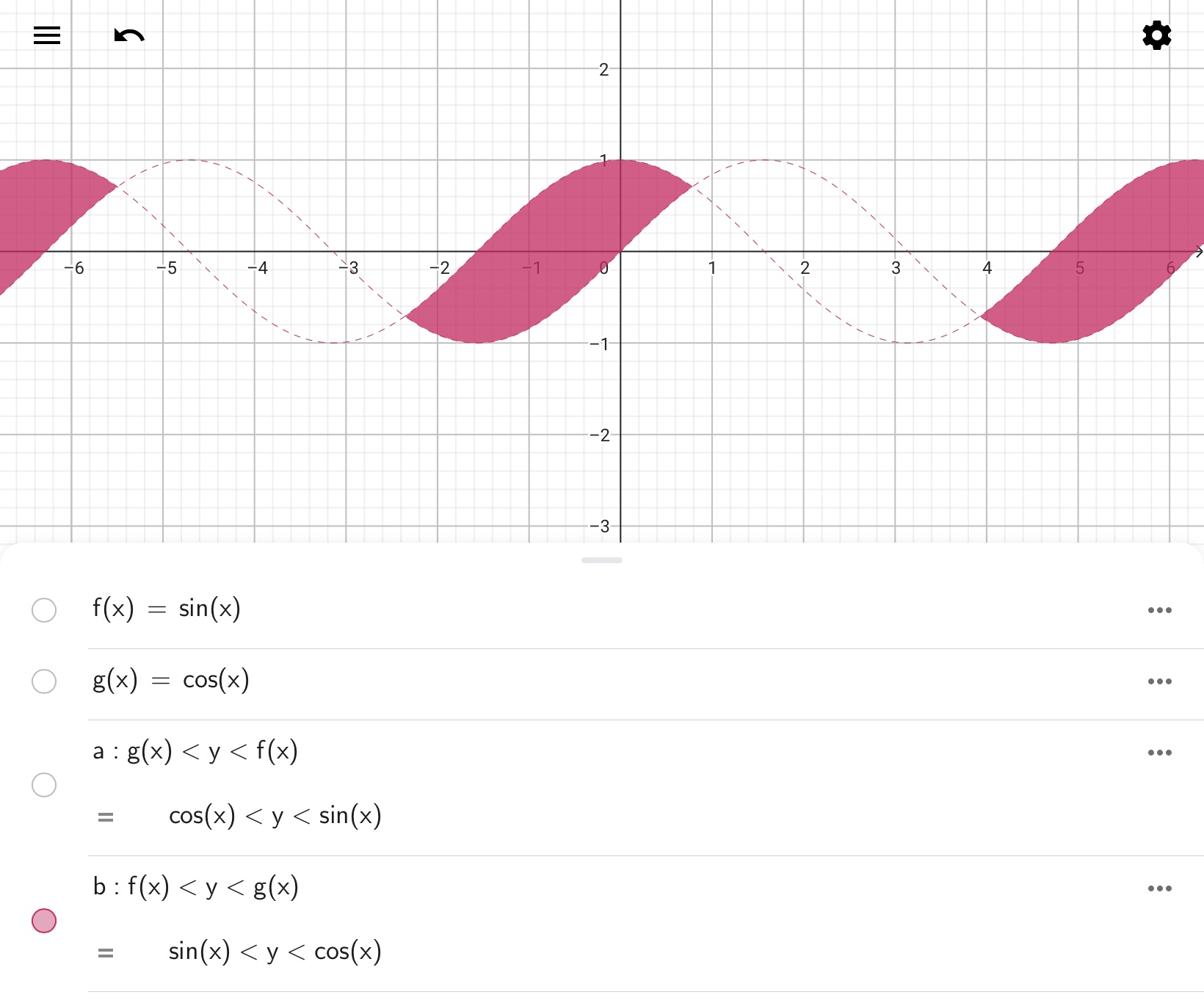
GeoGebraではOR演算(論理積演算)の演算子として∨、もしくは||が利用できます。先ほどの2つの領域に対してOR演算を実行すると、以下の出力が得られます。
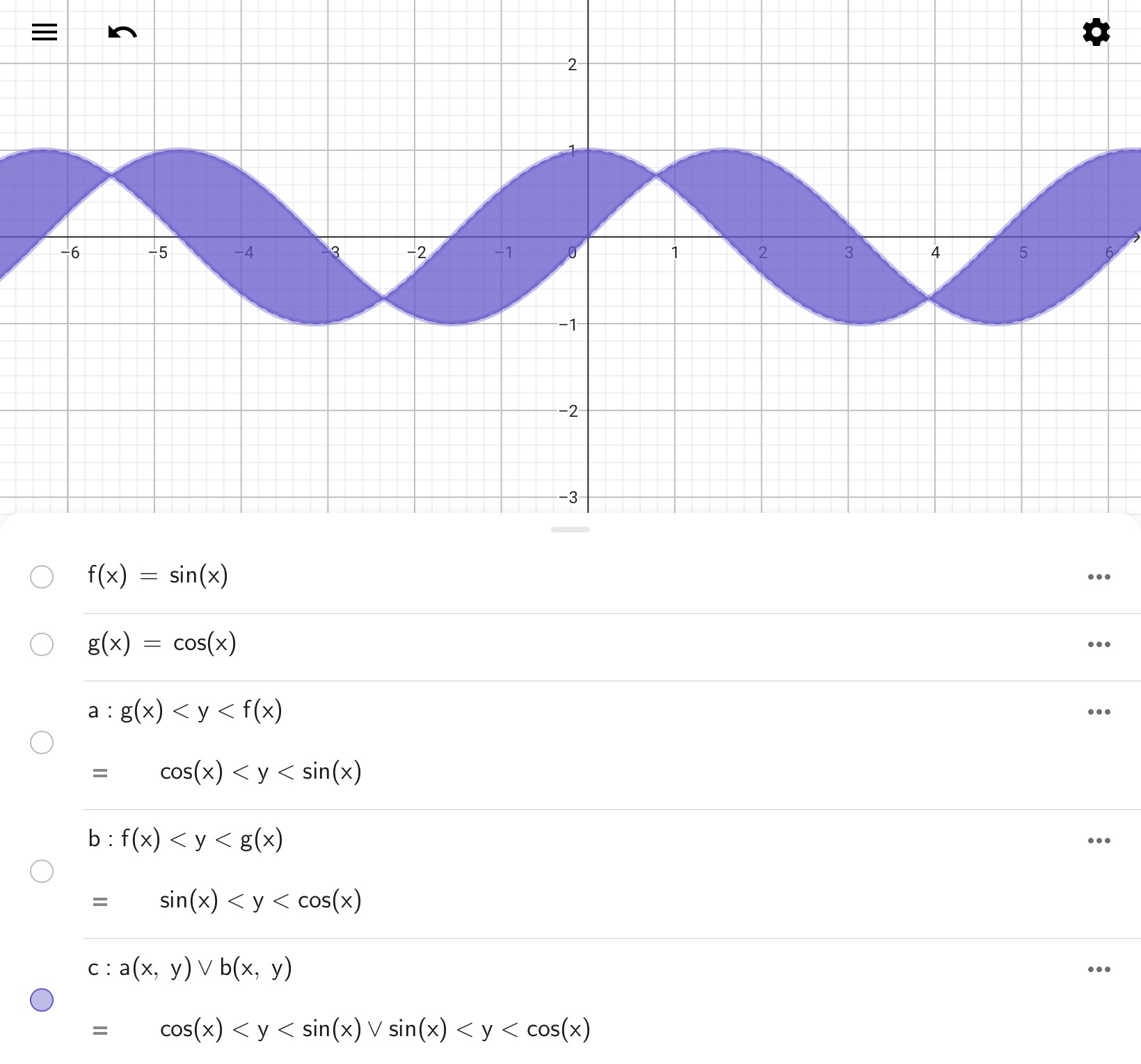
このように、OR演算を利用すると複数の不等式条件のいずれかを満たす範囲が描画できます。なお、図は示しませんが、AND演算とOR演算を組み合わせることもできます。
このようにGeoGebraは不等式オブジェクトを簡単に描画できます。工夫次第でかなり複雑なこともできるので、とてもオススメです
まとめ
この記事では無料の数学ソフトGeoGebraの幾何学的オブジェクトの中から、関数、媒介変数による曲線、不等式について説明しました。GeoGebraのようなグラフ計算ソフトを使うとさまざまな計算が簡単にできることがわかると思います。GeoGebraは数学への理解を深めるのに絶好のツールなので、ぜひ使ってみてくださいね。







