GeoGebraのオブジェクトを学ぼう(3)｜超速流！ケンヂ博士の理工学ライフ

前回の記事から、GeoGebraのオブジェクトについて説明しています。なお、この記事はGeoGebra公式サイト(オブジェクト関連ページ)をもとに作成されています。

前々回は「オブジェクトとはそもそも何なのか？」、「オブジェクトにはどんな種類があるのか？」という点について説明しました。GeoGebraのオブジェクトには一般的なものと幾何学的なものの2種類があります。

そして、前回の記事では、一般的なオブジェクトの基本である数、角度、複素数、ブーリアンについて説明しました。

今回の記事では一般的なオブジェクトの中から、リスト、行列、テキスト、画像について説明していきます。

一般的なオブジェクト

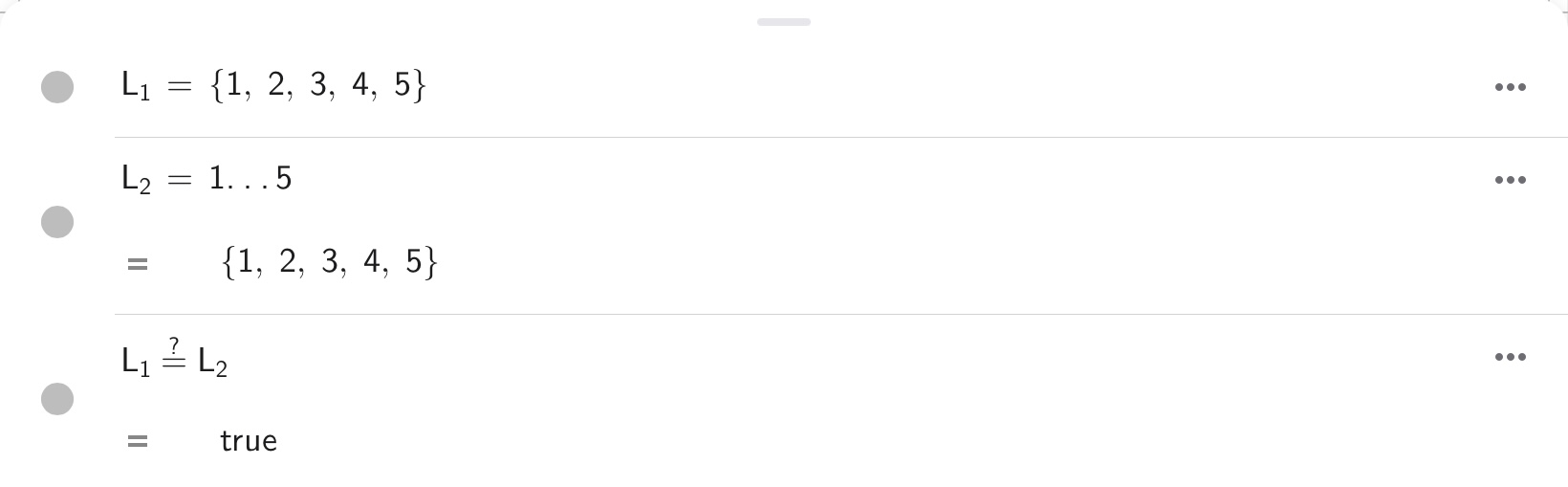
リスト\(L_1\)には5つの実数が含まれています。このリストの要素は1ずつ規則的に増加していっています。この場合、省略記法が使えて、1..5と入力しても同じ結果が得られます。リスト\(L_1\)とリスト\(L_2\)が等しいことを確認してください(※等値関係演算の出力がtrueになっています)。

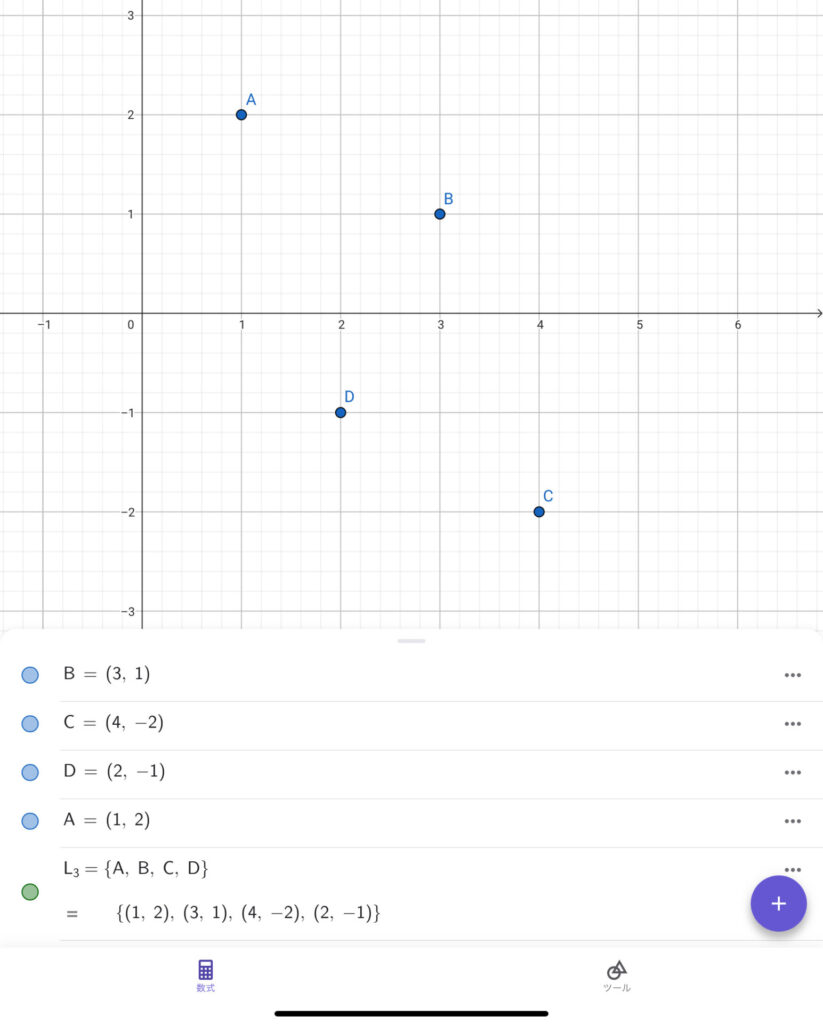
次は、複数の点をリストにまとめてみましょう。以下の例では、適当にプロットした4つの点A〜Dを\(L_3\)というリストにまとめています。

リストは何重にも入れ子にすることができます。つまり、「複数のリストをまとめたリスト」を作ることができるのです。例えば、L = {{{1, 2}, {3, 4}}, {{5, 6}, {7, 8}}}と入力すると3次元のリストを作ることができます。

種類の違うオブジェクトを1つのリストにまとめることもできます。以下の例では、数値と点と線分を1つのリストにまとめています。これはC言語で言うところの「構造体」に似た機能だと思います。関連する項目をひとかたまりにまとめておくと、プログラムの可読性が良くなることが多いです。リスト機能をうまく活用して、GeoGebraをスマートに使いこなしてくださいね。

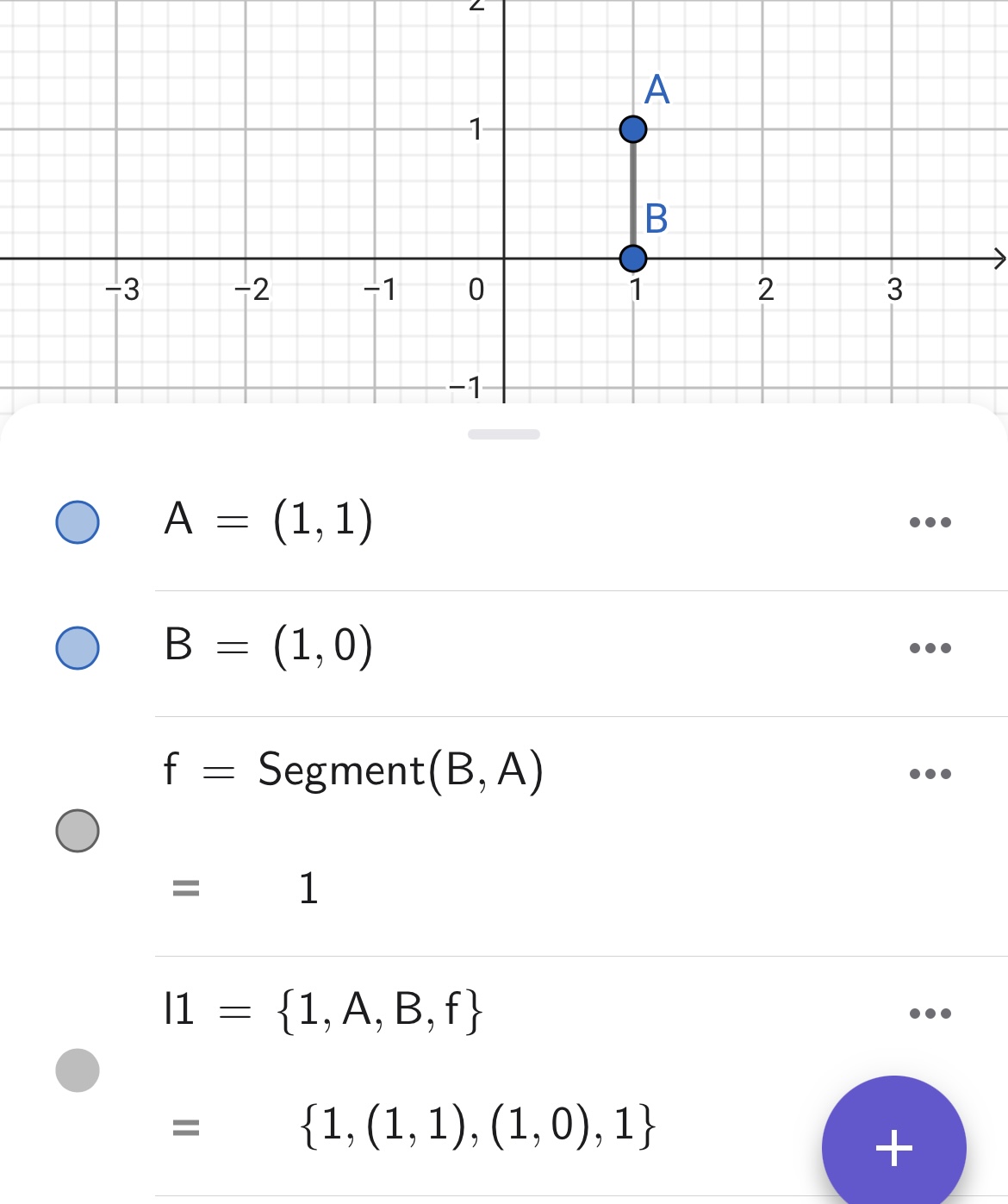
Notes: デフォルト状態の幾何アプリにおいて、リストは図示されません。

リストの各要素へのアクセス

リストの各要素にアクセスする方法は2種類あります。1つ目はElementコマンドを利用する方法、2つ目は次の例に示す簡易記法を利用する方法です。

Elementコマンド

Elementコマンド(Element( <List>, <Position of Element n> ))はリストの先頭から数えて，n番目の要素を取得するためのコマンドです。いくつか例を示しましょう。

Element({1, 3, 2}, 2)と入力した場合， {1, 3, 2}というリストの2番目の要素(つまり3 )が出力されます。
CASモードでElement({a, b, c}, 2) と入力した場合，{a, b, c}というリストの2番目の要素（つまりb）が出力されます。

リストが多次元であった場合，アクセスしたい場所をより細かく指定することも可能です。その場合はElement( <List>, <Index1>, <Index2>, …)と入力してみてください。例えば，3次元のリストL = {{{1, 2}, {3, 4}}, {{5, 6}, {7, 8}}}に対して，Element(L, 1, 2, 1)と入力した場合，3が出力されます。また，Element(L, 2, 2) と入力した場合は{7, 8}が出力されます。

多少説明が前後しますが，リストが行列であった場合，Element( <Matrix>, <Row>, <Column> )と入力することで，行列から要素を取り出すことができます。

なお，Elementコマンドを使う場合、リストの全要素数よりも大きい数やゼロ以下の数をアクセス先として指定することはできません。また，Elementコマンドでは「リストの末尾から数えてm番目の場所にアクセスする」ということはできないようです（筆者が公式Wikiを調べた範囲ではそのような記述はありませんでした）。

簡易記法

リストや行列のオブジェクト名の後に(<Position of Element n>) と入力しても，リストや行列の要素にアクセスすることができます。

例えば，list = {1, 2, 3, 4, 5}という1次元のリストがあるとします。このリストの要素に簡易記法でアクセスしてみましょう。このリストへのアクセス例を以下に示します。

list(1)と入力するとリストの先頭から1番目の要素である 1が出力されます。
list(2)と入力するとリストの先頭から2番目の要素である 2が出力されます。
list(0)は未定義です。

なお，GeoGebraの公式Wikiには以下のような記述がありますが，筆者が確認したiPad版の環境では下記の記法は使用できませんでした(※動作環境によって違いがあるのかもしれません)。

list(-1)と入力するとリストの末尾から1番目の要素である 5が出力されます。
list(-2)と入力するとリストの末尾から2番目の要素である 4が出力されます。

行列に対しても簡易記法は有効です。行列のオブジェクト名の後に(<Row>, <Column> )と入力すれば，行列の要素にアクセスすることができます。

リストに対する演算

リストに対して下記の演算子やリストコマンドを適用することができます。

演算内容	入力バー	例
Belongs to(元として含む、属する)	∈	a ∈ list1
Subset (部分集合)	⊆	list1 ⊆ list2
Proper subset(真部分集合)	⊂	list1 ⊂ list2

集合関連の論理演算

また，<List1> \ <List2>と入力すると， List1とList2の差分リストを作ることができます。

要素数が同じ2つのリストに対しては，四則演算を実行することができます。つまり，List1 + List2やList1 – List2、List1 * List2、List1 / List2といった演算を実行できます。基本的に四則演算はリストの要素ごとに実行されますが、乗算に関してはすこし注意が必要です。リストが行列として解釈でき、行列の乗算が実行できる場合、要素ごとの乗算ではなく行列の乗除算が実行されます。

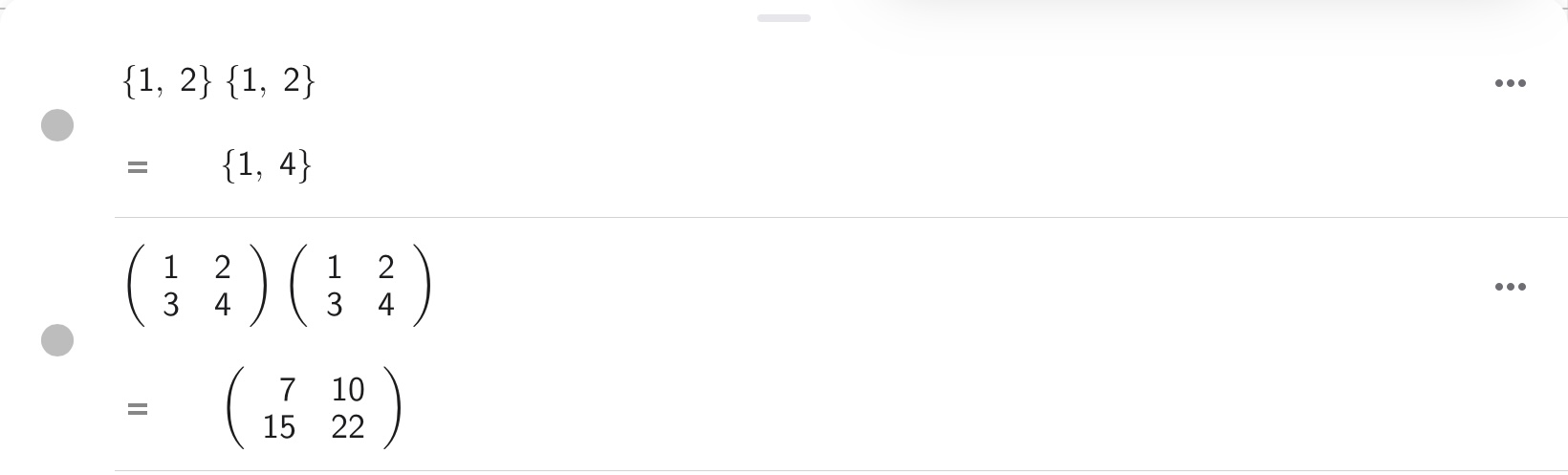
例えば、{1,2}×{1,2}と入力すると演算結果は{1,4}になりますが、{{1,2},{3,4}}×{{1,2},{3,4}}と入力した場合、これは行列の乗算と解釈できますので、演算結果は{{7,10},{15,22}}になります(※{{1,4},{9,16}}にならないことに注意してください)。

Note: ベクトルの内積を計算したい場合はこちらのページをご覧ください→ Vector product

リストの各要素に対して、同じ数値を加算・減算・乗算・除算することもできます。List + Number,List – Number,List * Number,List / Number,Number / Listというように入力してください。

リストを使うと、複雑な計算処理をシンプルに記述できることがあります。以下はリストを用いた演算例です。

List ^ 2 リストの各要素を2乗する。
2 ^ List 2の累乗のリストを作成する。ただし、指数はListの要素によって決まる。
List1 ^ List2 List1 とList2の各要素を用いて、a^bを計算する。
sin(List)Listの各要素に対してsin関数を計算する。

リストの使い方をよく学んで慣れておくと何かと便利だと思います。

リストの比較

2つのリストを比較したい場合は以下のように入力します。下記の演算の判定結果はいずれもブーリアン(true or false)で出力されます。

2つのリストが完全に一致するかどうかを調べたい場合は，List1 == List2もしくはList1 != List2と入力します。
リストには同じ要素が重複して含まれていることがあります。2つのリストのユニークな要素が一致するかどうかを調べたい場合はUnique[list1] == Unique[list2] もしくは list1 \ list2 == {}と入力します。
リストに含まれる要素の順番を無視して比較したい場合はSort[list1] == Sort[list2]と入力します。

リストの比較についてより深く知りたい方はUniqueコマンドやSortコマンドについて調べてください。

行列

GeoGebraではリストを用いて行列を表現できます。そして、その行列に対してさまざまな演算を行うことができます。

行列の定義方法

行列を定義するには、「リストのリスト」を作れば良いです。例えば、3×3行列を作りたい場合、 {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}というように入力します。{1, 2, 3}や{4, 5, 6}、{7, 8, 9}はそれぞれリストになっています。これらのリストを中括弧に入れて、さらにリスト化すると行列になります。

NOTE: 幾何アプリで画面上に行列を表示したい場合、FormulaTextというコマンドを使うと良いです。

行列の要素へのアクセス

行列の各要素へアクセスする方法は、リストの各要素にアクセスする方法と同じです。つまり、Elementコマンドを利用する方法と、簡易記法を利用する方法です。これに関してはすでに説明しましたので、復習したい方はこちらをクリックしてください。

行列の演算

GeoGebraでは行列に対してさまざまな演算を行うことができます。四則演算など、リストの項目で説明した一連の演算はもちろん、各種のMatrixコマンドを利用することができます。Matrixコマンドの代表例は以下のとおりです。

Determinant[Matrix]: 行列式を計算する。
Invert[Matrix]: 逆行列を計算する。
Transpose[Matrix]: 転置行列を計算する。
ApplyMatrix[Matrix,Object]: 点やベクトルといったオブジェクトに対して、行列を作用させる。
ReducedRowEchelonForm[Matrix]: 行列を行階段形に変形する。

テキスト

GeoGebraでは、テキスト(文章)をオブジェクト化することもできます。テキストをオブジェクト化して表示させることで、教材が分かりやすくなったり、自分の計算の意図を他の人に伝えやすくなります。

テキストオブジェクトを作るには二重引用符（ダブルクオーテーションマーク）“”でテキストを挟めば良いです。テキストオブジェクトを画面に表示させるには、Textコマンドを使います。数式をテキスト化して表示するFormulaTextのようなコマンドもあります。

テキストオブジェクトには3種類あります。1つ目はStatic text(静的なテキスト)です。2つ目はDynamic text(動的なテキスト)、Mixed text(混合テキスト)です。この3つの違いについて簡単に説明します。以下の画像を見てください。

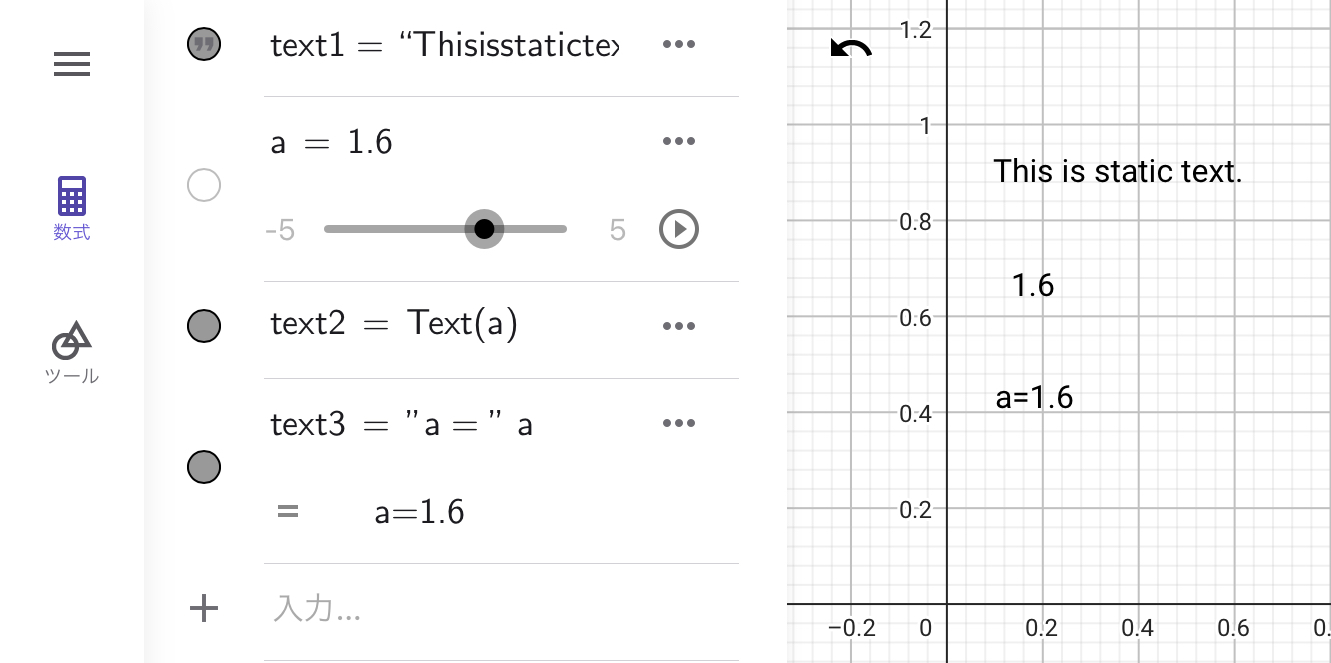
text1=”This is static text.”と入力するとtext1というオブジェクトが定義されます。次に、aという数値オブジェクトを定義します。aはスライダーで変更することができます。ここでtext2=Text(a)と入力すると、aに代入されている数値(下の画像では1.6)がテキスト化され、text2というオブジェクトになります。text2はaという他のオブジェクトに紐づけられているため、aが変更されると、text2も同時に変更されます。一方、text1は他のオブジェクトに紐づいていないため、他のオブジェクトが変更されてもその影響を受けません。

このように、他のオブジェクトの変更の影響を受けないテキストオブジェクトのことを「静的テキスト」といいます。また、他のオブジェクトが変更された時に、変更の影響を受けるテキストオブジェクトのことを「動的テキスト」といいます。「静的テキスト」と「動的テキスト」を組み合わせたテキストのことを「混合テキスト」といいます。たとえば、text3=“a=”aと入力すると、text3はa=1.6のような形で表示させることができるようになります。スライダーでaを変更すると、text3は右辺の値だけが変化します。

テキストオブジェクトを効果的に使えば、わかりやすい数学教材を作りやすくなりますので、ぜひ活用してみてください。

画像

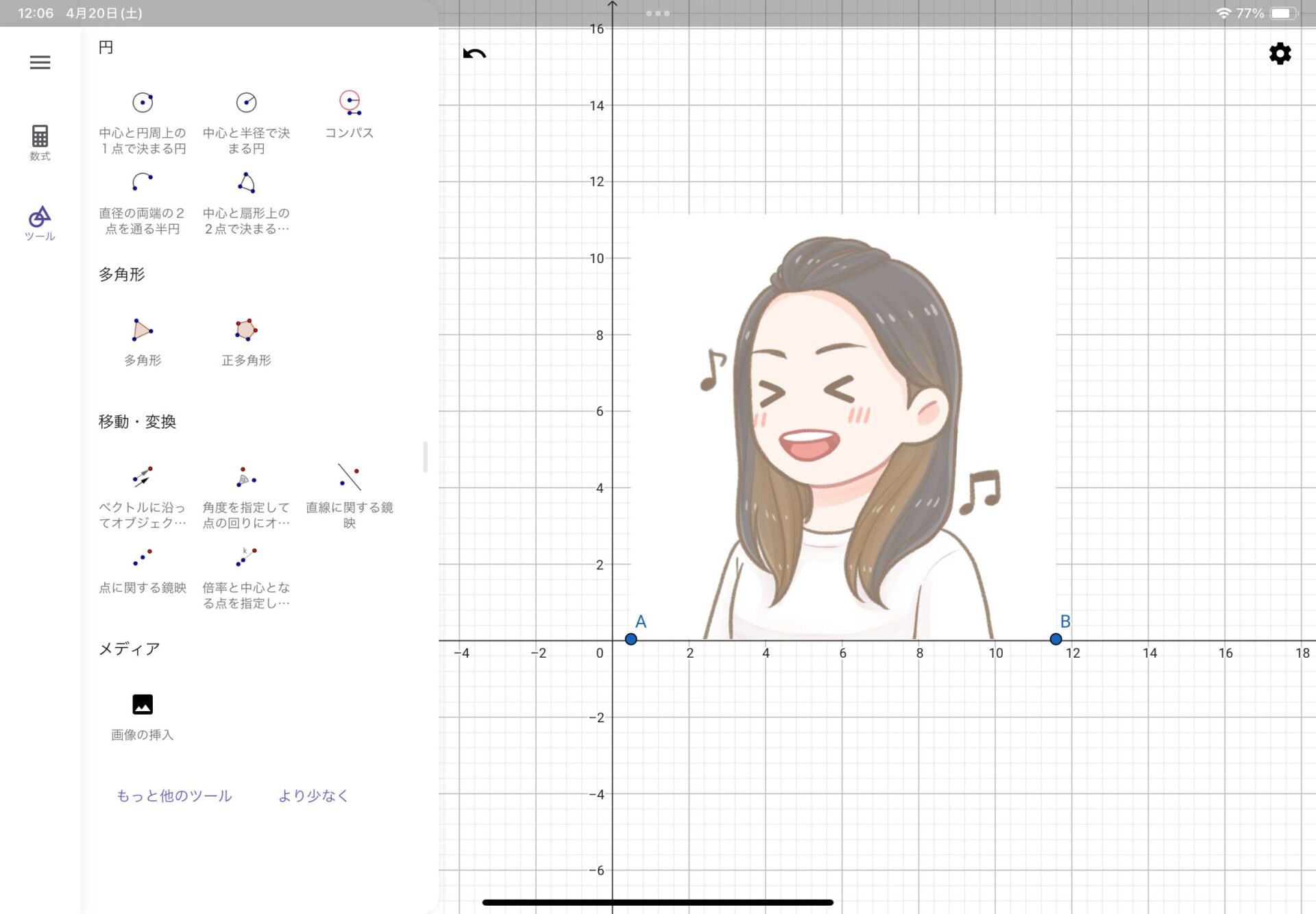
GeoGebraの幾何アプリでは画像をオブジェクトとして取り込んで表示することもできます。ツールメニューから「メディア→画像の挿入」を選択してください。

以下に、画像オブジェクトの例を2つ示します。画像を挿入すると、挿入された画像の左下と右下の頂点の2点が画像オブジェクトに紐付けられます。この2点をマウス操作(タブレットの場合、タッチ操作)で動かすことによって、画像の位置や大きさ、角度を変えることができます。

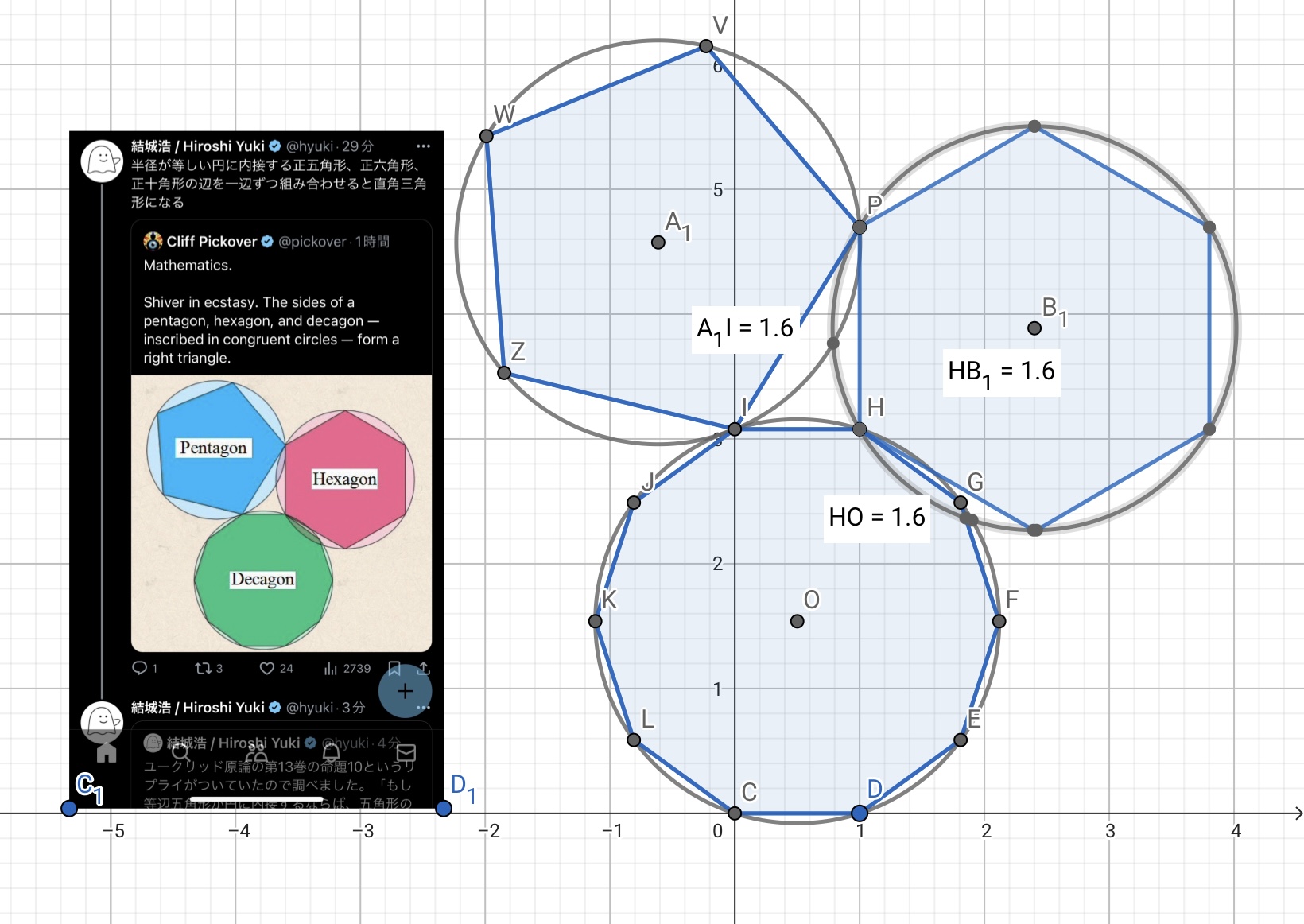
GeoGebraの公式wikiでは画像オブジェクトの活用法についてあまり説明がありませんが、想像力次第でさまざまななことができるオブジェクトだと思います。

まとめ

今回の記事ではGeoGebraの一般的なオブジェクトの中から、リスト、行列、テキスト、画像について説明しました。リストや行列を理解すれば、GeoGebraでさらに複雑な計算を行うことが可能になります。また、テキストオブジェクトや画像オブジェクトを活用すれば、GeoGebraで行った計算や作業の結果を他の人にわかりやすく説明することが可能になります。

一般的なオブジェクトの説明は以上です。次回からは幾何オブジェクトについて解説していきますので、ご興味のある方は是非そちらもご覧ください。

GeoGebra グラフ計算機コンピュータ数学

GeoGebraのオブジェクトを学ぼう(3)

一般的なオブジェクト