このサイトではGeoGebraやDesmosといったグラフ計算機ソフトの解説を行うことが多いです。今回はグラフ計算機ソフトGeoGebraを使って、代々木ゼミナールの有名な数学講師 荻野暢也先生が解説していた「接点t」の問題を解いてみます。
接点tの問題とは?
この問題で取り扱う接点tの問題とは以下のようなものです。
三次関数\(y=x^3-3x\)に対して、\(xy\)座標上の任意の点\(a,b\)を通過する接線を考える。点\(a,b\)を通過する接線が3本存在するためには、\(a,b\)がどのような位置にあれば良いか、答えよ。
一見、なんの変哲もない高校数学レベルの微分の問題ですが、この問題が有名になったのにはきっかけがあります。それは20年ほど前に流行したこの動画です。
これは2004年に代々木ゼミナールが試聴動画としてインターネット公開した数学の授業風景です。この講義をした数学講師は荻野暢也先生という方なのですが、予備校のイメージを覆すような型破りなパフォーマンスが印象的です。講義の特徴として、
- テンションが上がると急にタメ口になる
- ガラの悪い、怖いお兄さんがプッツンしているような喋り方
- 何故か教壇に足を乗せる
- 時折混じる、どことなく哲学的な物言い
のようなものがあります。
荻野先生の「接点t」の動画が大型匿名掲示板で話題になったのを機に代ゼミ講師陣の奇抜さが知れ渡るようになり、以後他校を含め様々な講師がネットで名を上げたそうです。当時はFLASH黄金時代だったこともあり、荻野先生の音声はFLASHや音MADの素材としてもてはやされました。
「接点t」「この点は出ねぇよぉ!」「ゆうやく(誘惑)振り切ってこうだ」「誘惑に負けてy=mxなんて置いちゃう輩が多いんだよね」「4個3本」「ぉーん」などの名台詞(迷台詞?)に懐かしさを感じる方もいるかもしれません。個人的には、「所詮、手際よく解けるように作られた入試問題という 箱庭の中でしかぁー、いっ、生きていけない解答に過ぎないんだ。」というセリフが好きですね。
さて、荻野先生がこの有名な動画で説明されているのが、この三次関数の微分の問題なのですが、内容を正確に理解されている方はどの程度いるでしょうか?これ実は結構、面白い問題なんですよね。今回、私はGeoGebraを使ってこの「接点t」の問題を解説してみたいと思います。
点と三次関数のグラフを描く
まず、問題の内容を理解するために、点と三次関数\(y=x^3-3x\)のグラフを描いてみましょう。GeoGebraでこれらの点やグラフを描くのは簡単です。点を描く方法はいくつかありますが、ここでは\(A=(a,b)\)と入力します。また、グラフを描くには\(y=x^3-3x\)と入力します。上手くいけば、以下のようなグラフが描けるはずです。
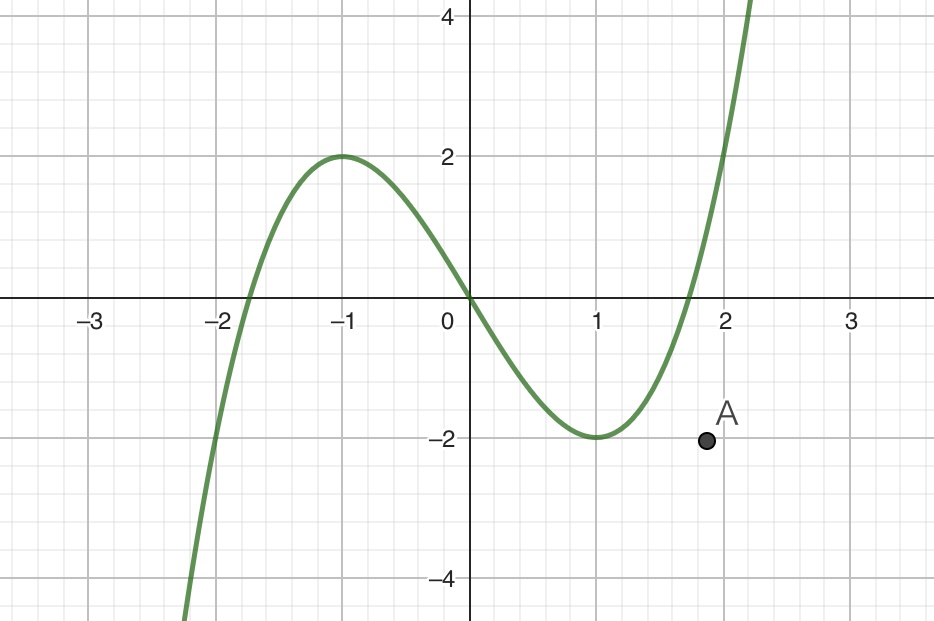
数式を入力するだけで複雑なグラフを一瞬で描画できるのがグラフ計算ソフトのすごいところです。なお、GeoGebraでは、点Aをマウス操作やタッチ操作で自由に移動させることができます。ここでは適当な位置に点Aをおいています。
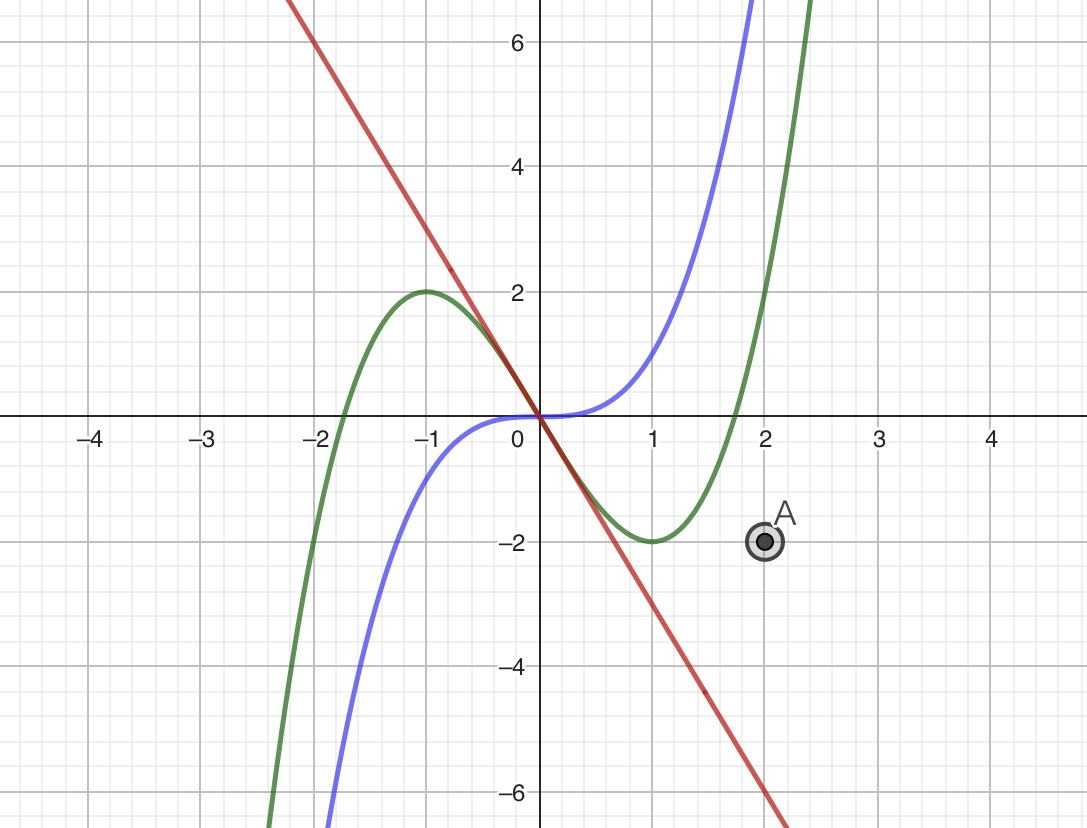
さて少し横道にそれますが、本題に入る前にこの問題で取り扱う三次関数\(y=x^3-3x\)の性質について簡単に説明しておきましょう。このグラフは三次関数\(y=x^3\)と一次関数\(y=-3x\)の和です。\(x\)が0近傍の範囲では\(y=x^3-3x\)は一次関数\(y=-3x\)にほぼ等しいですが、\(x\)が0から遠ざかるにつれて\(y=x^3\)に近づいていきます。グラフ計算ソフトを使えば、こういったグラフの特長も簡単に把握することができます。
接線を引いてみる(問題の意図を把握する)
グラフの概形がわかったので、次は適当に接線を引いてみます。「関数の接線」というのは簡単にいうと、「ある点において、関数と一点で接触する直線」のことです。より厳密な定義は以下のようなものですが、ピンとこない方は読み飛ばしていただいても構いません。
解析幾何学において、与えられた直線が曲線\(y=f(x)\)の \(x=c\)(あるいは曲線上の点 \((c, f(c)\))における接線であるとは、その直線が曲線上の点\((c, f(c)\)を通り、傾きが\(f\)の微分係数\(f'(c)\)に等しいときに言う。
さて、先ほどの点Aに対しては3本の接線が引けます。GeoGebraで関数の接線を引く方法は後ほど解説したいと思いますが、一本めは以下のような直線です。
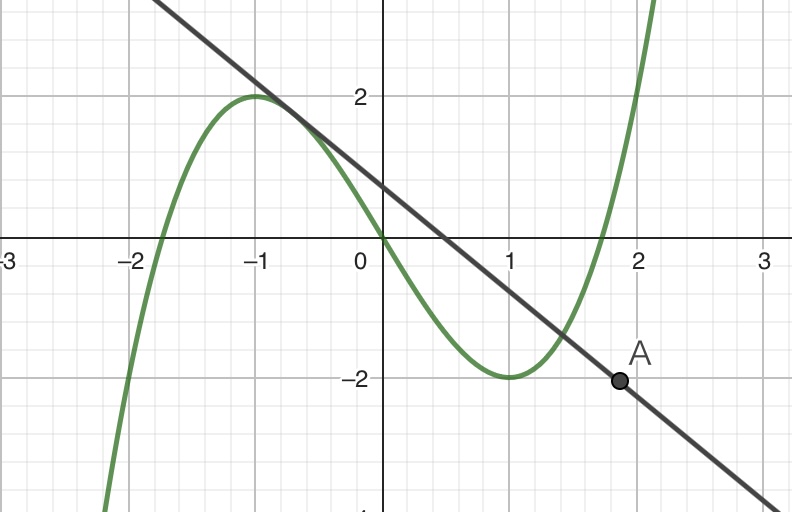
同じように2本めの接線を引いてみます。
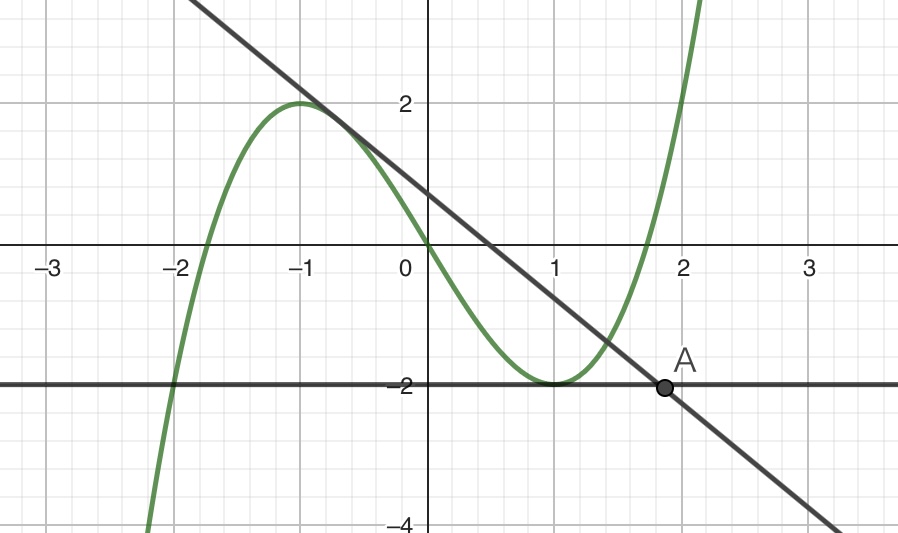
3本めの接線も引きます。
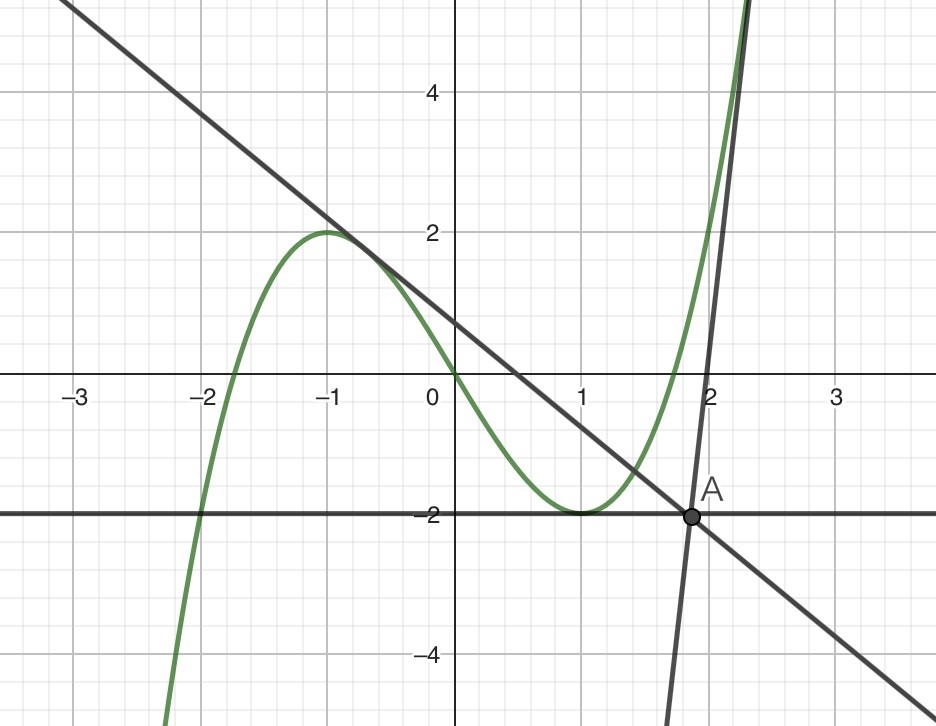
このような形で、点Aを通過する3本の接線が引けました。
しかし、どのような点に対しても、その点を通過する接線が常に3本引けるというわけではありません。例えば、以下の図に示す点Bを考えてみましょう。点Bを通る接線は1本しか引くことができません。
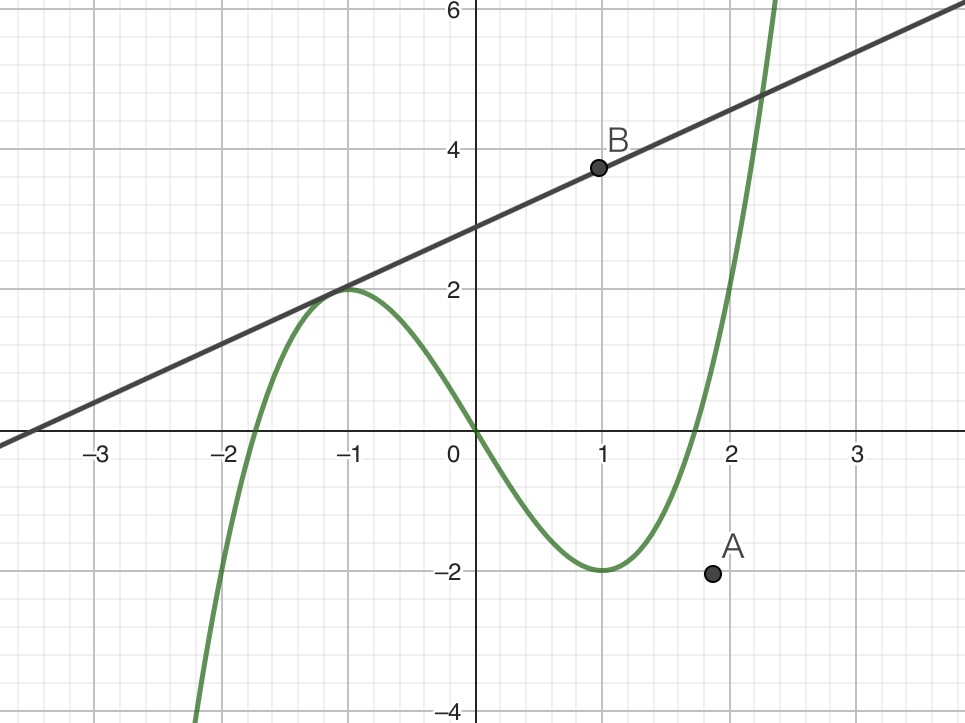
このように、\(xy\)平面上における任意の点を通過する三次関数\(y=x^3-3x\)の接線の本数は、点の位置によって変わってくるのです。そのため、この問題では「点の位置がどこにあれば接線が3本引けるか?」ということを問うています。
実験してみる
点の位置によって接線の本数が変わることが説明できたので、それでは実際に問題を解いてみましょう。ただ、この問題はもともと大手予備校で解説されるような大学入試レベルの難問です。この難問をわかりやすく説明するために、まずは実験的な解き方をやってみましょう。
この問題の解き方はいろいろあると思いますが、GeoGebraのようなグラフ計算機を用いてもよい場合、地道に点を動かしながら、接線の本数を調べていく……という実験的な方法を取ることができます。大学入試など、制限時間内に自分の頭だけで答えを出さなければいけない状況では使えない方法ですが、この問題だとこういった実験的方法がすごく有効だったりします。
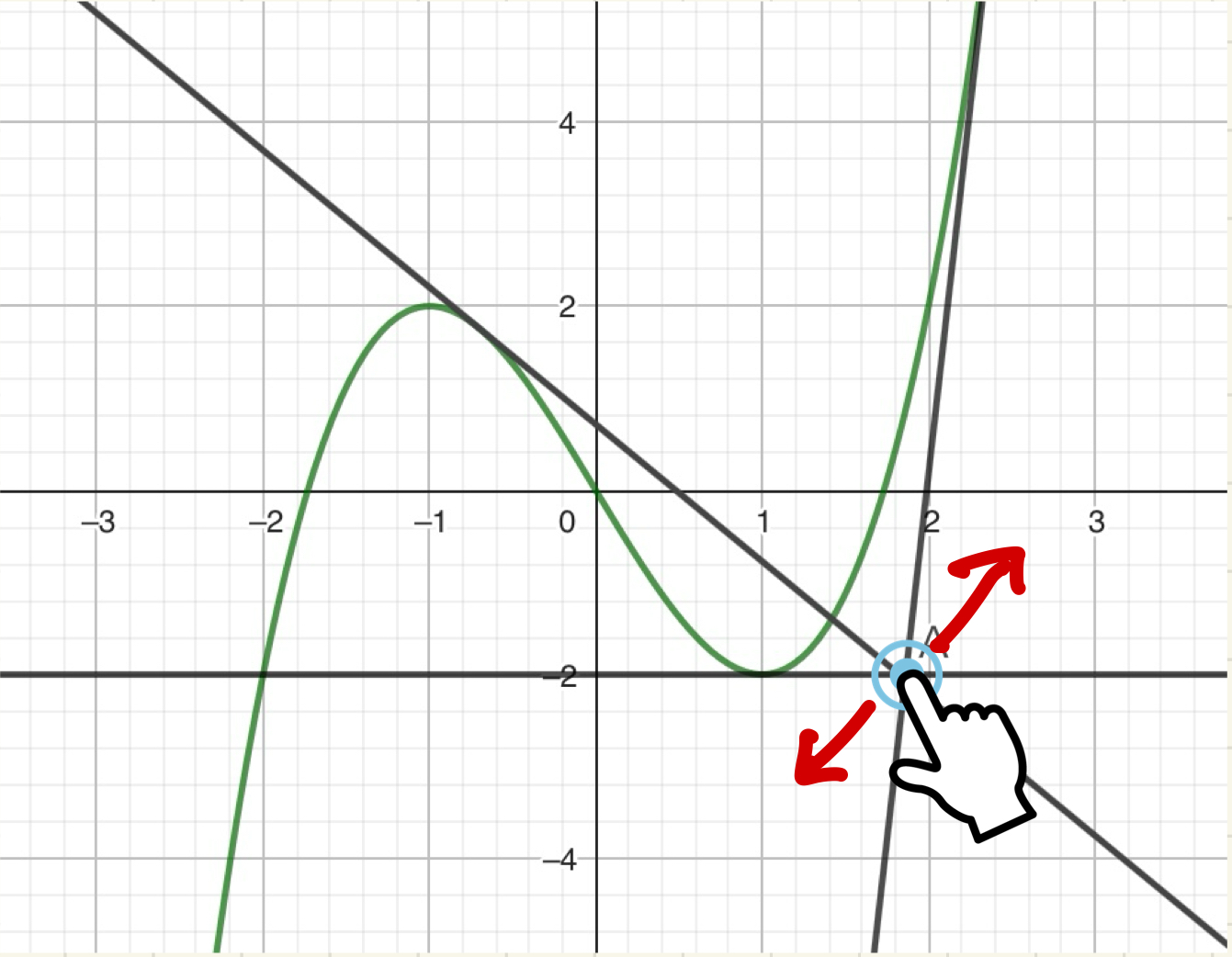
この実験作業は手動でやってもいいですし、コンピュータを使って自動でやらせても良いです(プログラミングの知識が必要になりますが、さほど難しくはないです)。実際に点を動かしながら実験してみると、短時間で答えに到達することができます。この問題の答えは下図のようになります。大学入試での模範的解答とは異なる部分が多いですが、実用的にはこれも立派な解答だと思います。
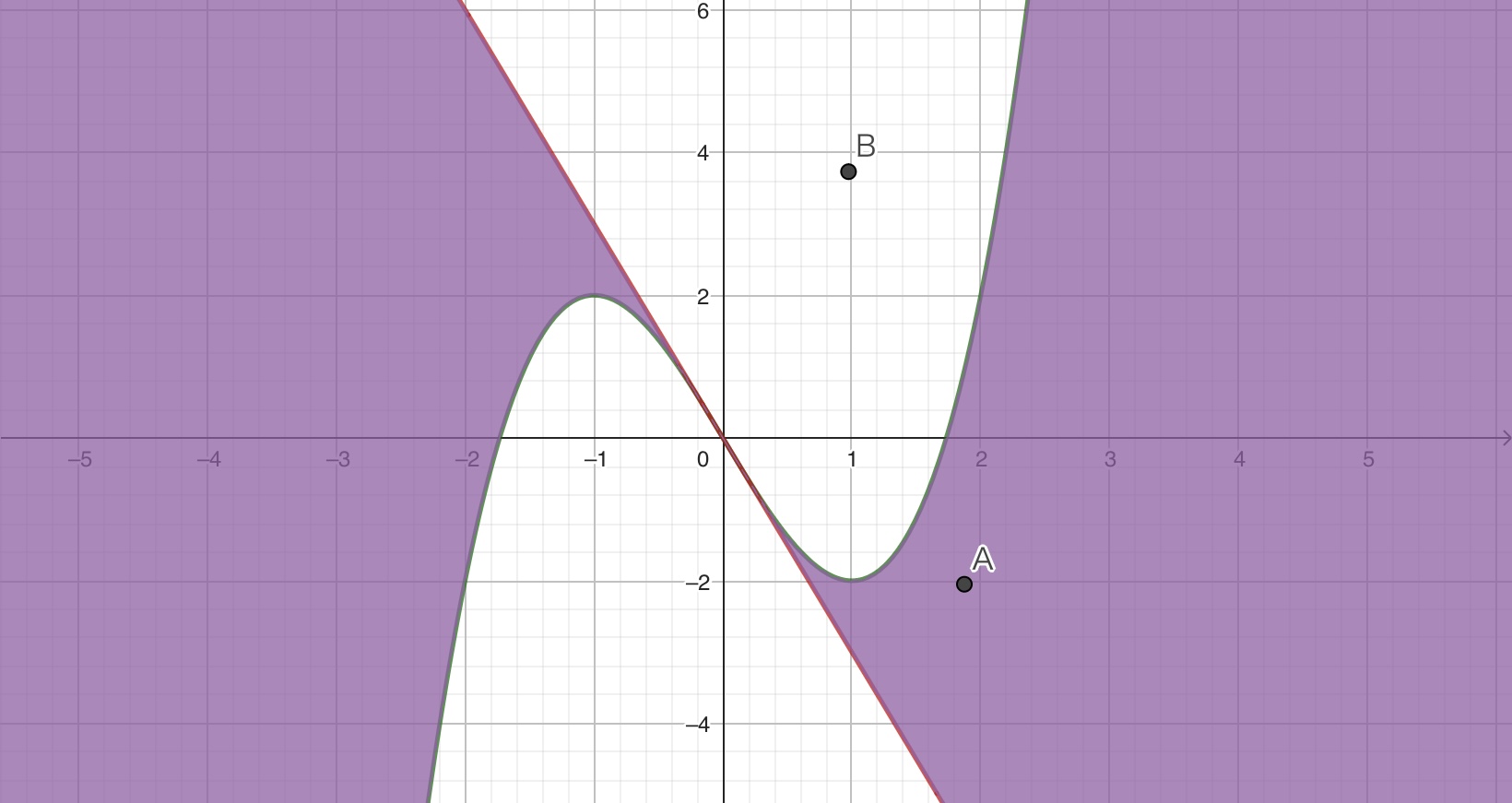
GeoGebraのようなグラフ計算機ソフトはこういった実験作業がとてもやりやすいという特徴を持っています。ぜひ実際に触って、その良さを体感してみてください。
接線の方程式を考える
実験的な解法でも答えは出せるのですが、実験的な方法の難点は「実験データから導き出された答えはあくまでも予想に過ぎない(厳密な証明になっていない)」ことです。証明ができていないことです。この問題の厳密な答えを知るには、荻野先生の講義ででてきた「接線の方程式」について考えるのが近道です。
ということで、接線の方程式について考えてみましょう。曲線\(y=f(x)\)の\(x=c\)における接線は、媒介変数\(t\)を利用すると以下の式で書くことができます。
$$ \begin{bmatrix} x\\ y\\\end{bmatrix} = \begin{bmatrix} c\\ f(c)\\\end{bmatrix}+t \begin{bmatrix} 1\\ f’(c)\\\end{bmatrix} $$
ここで、\(f'(c)\)は\(x=c\)における曲線\(f\)の微分係数(傾き)です。この数式は曲線上の点\((c, f(c)\)を通り、傾きが\(f'(c)\)に等しい直線(すなわち、\(x=c\)における接線)を意味します。なお、荻野先生の講義では\(t\)という記号で接点を表していましたが、ここではGeoGebraのようなグラフ計算機を使う都合上、媒介変数を\(t\)とします。
この方程式をGeoGebraに入力して、接線のグラフを描いてみます。まずは関数を入力しましょう。ここでは\(y=f(x)=x^3-3x\)なので、以下のように入力します。
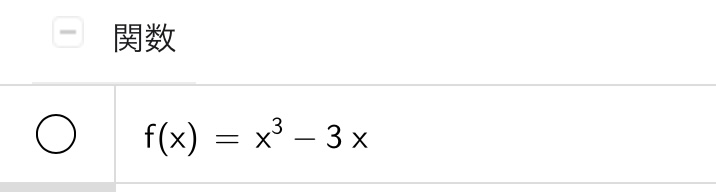
次は関数を微分します。GeoGebraでは以下のようにダッシュ記号をつけると微分が計算されます。

その次は接線がどの位置で三次関数と接するかを指定するための数値オブジェクトを作ります。ここでは接線を3本引きたいので、数値オブジェクトを3つ作ることにします。数値オブジェクトの名前は自由に設定して良いですが、ここでは\(l,m,n\)にしましょう。ここでは以下のようにスライダー機能を使って\(l,m,n\)を自由に変更できるようにします。
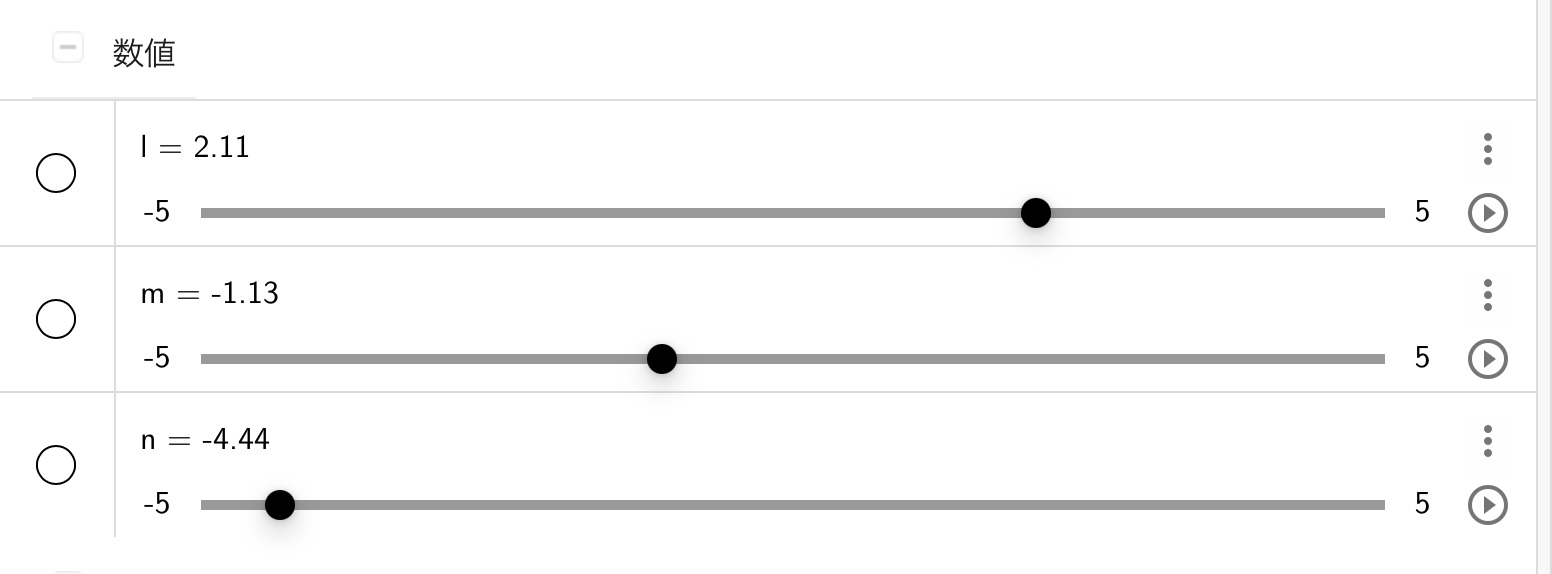
あとは先ほどの媒介変数を使った接線の方程式をGeoGebraに入力するだけです。以下の図は方程式の入力例です。\(l,m,n\)という数値オブジェクトを方程式に入れておくと、\(l,m,n\)を変更した時に方程式が再計算されるのでとても便利です。

あとは接線が点Aを通過するように\(l,m,n\)の数値を調節してあげれば、以下のグラフが書けます。\(x=l,m,n\)の各点で直線が三次関数のグラフと接することを確認してください。

ちなみに先ほどの接線の方程式から媒介変数\(t\)を消去すると以下のような数式が得られますので、この数式を使って接線のグラフを描いても良いです。
$$ y = f’(c) x +\{f(c) – c f’(c) \}$$
また、ここで\(y=f(x)=x^3-3x\)、\(y=f’(x)=3x^2-3\)であることを使えば、以下の数式が得られます。これを使って接線のグラフを描いても良いです。
$$ y = (3c^2-3) x +\{(c^3-3c) – c (3c^2-3) \}$$
これで、ご紹介した接線の方程式が妥当であることをGeoGebraで確認できました。
任意の点を通過する接線について考える
さて、ようやく本題ですが、次は任意の点\( (a,b) \)を通過する接線について考えましょう。
先ほどの\(x=c\)で三次関数と接する接線の方程式をもう少し整理すると、\(c\)に関する以下の三次方程式が得られます。
$$ 2c^3 -3 x c^2 +(3x + y) = 0$$
数式を変形する際、ミスしそうだったので、私はGeoGebraのCASモード(数式処理機能)を使って計算しました。
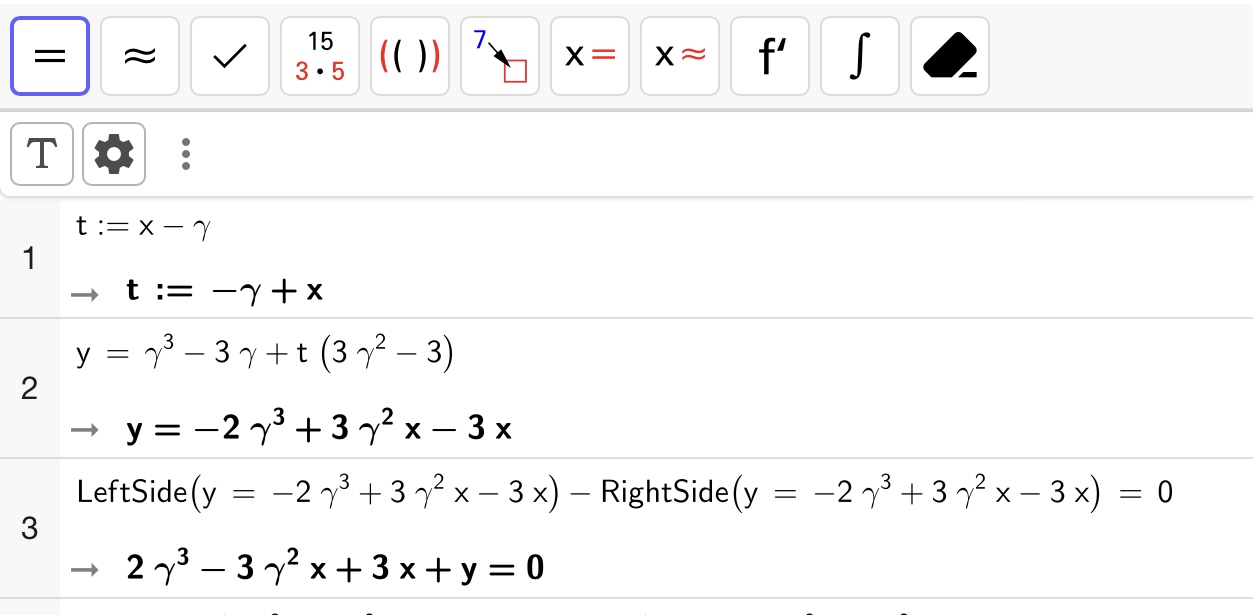
上の画像では\(c\)の代わりに\(\gamma\)という記号を使っていますが、そのことに深い意味はありません。
先ほどの式に\(x=a,y=b\)を代入すると、以下のようになります。
$$ 2c^3 -3 a c^2 +(3a + b) = 0$$
ここで\(c=x\)と変数を置き直すと、以下の数式が得られます。
$$ 2x^3 -3 a x^2 +(3a + b) = 0$$
これが任意の点\( (a,b) \)を通過し、三次関数と接する接線がどこで三次関数と接するかを表す式です。
さて、次はこの式と\(y=f(x)=x^3-3x\)の関係について考えてみます。先ほどの式の左辺を\(p(x)\)と置き、\(y=p(x)=2x^3 -3 a x^2 +(3a + b)\)のグラフを描いてみます。せっかくなので、\(y=f(x)=x^3-3x\)のグラフと重ねて描いてみましょう。GeoGebraにこれらの式を入力すると以下のグラフが書けます。
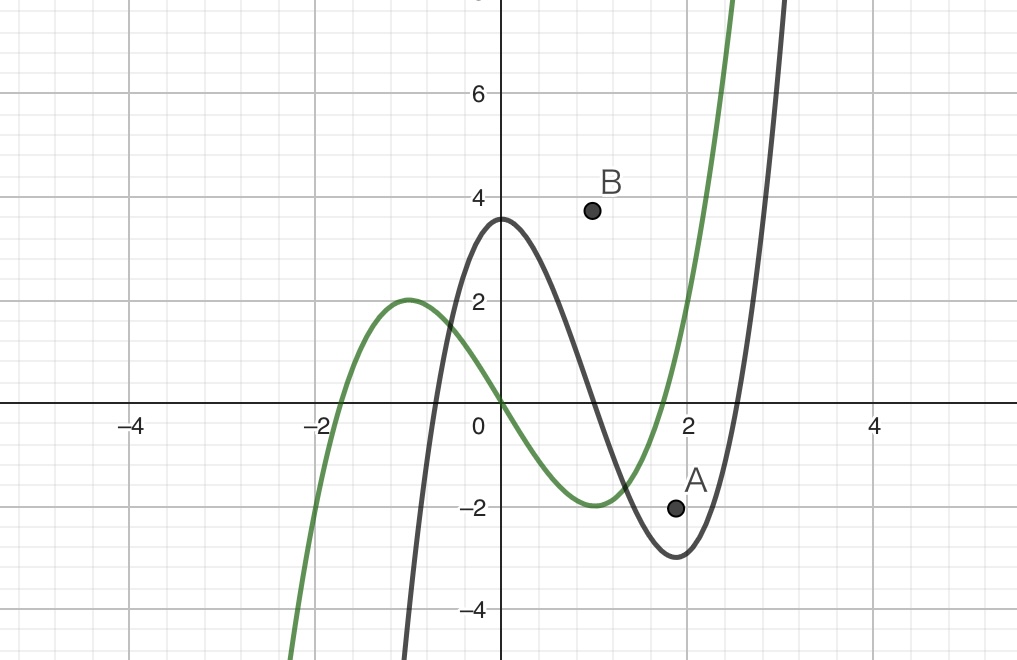
それでは以下の図のように、関数\(p(x)\)がゼロになる点をO、P、Qとそれぞれ置き、そこから\(x\)軸に垂直な直線を引きます。そして、それらの直線と関数\(f(x)\)の交点をR、S、Tとそれぞれ置きます。
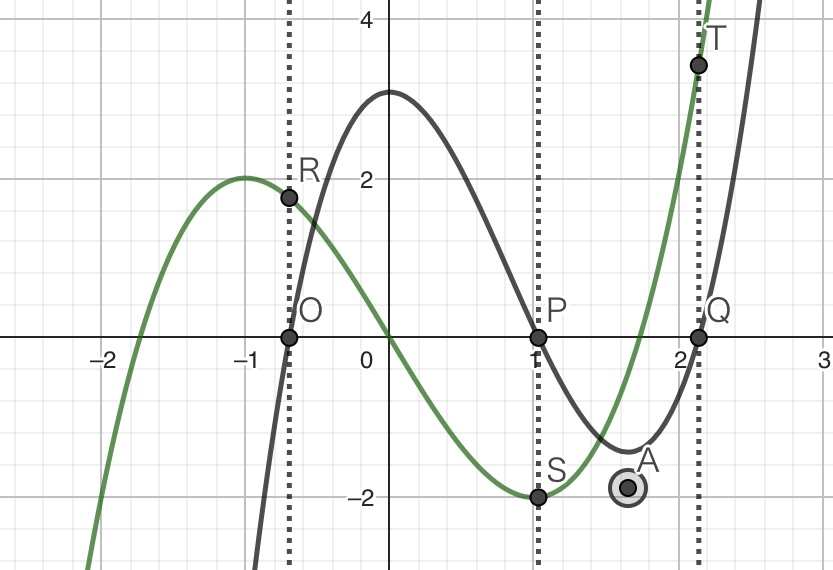
そして、点R、S、Tと点Aを結ぶ直線をそれぞれ描画してみると、以下の図が描けます。R、S、Tは点Aを通過する接線の接点であることが以下の図からわかると思います。
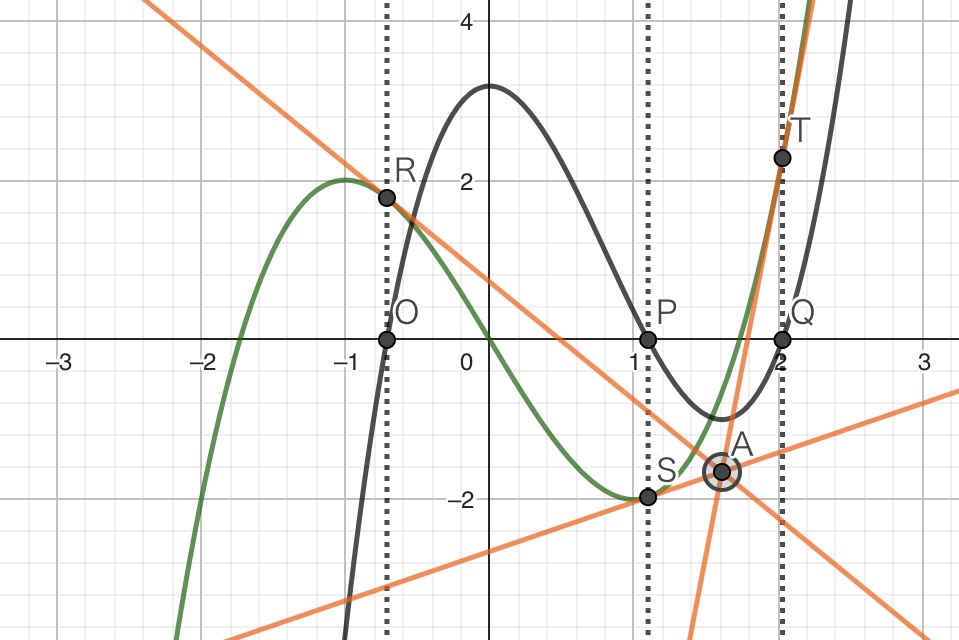
このようにGeoGebraの各種ツールを使って接線を引くと、点Aを移動させると接線も連動して変化します。例えば、点Aを下図の位置に移動させてみます。そうした場合、接線は1本になってしまいます。この位置では\(p(x)=0\)が成立するポイントが一つしかないからです。
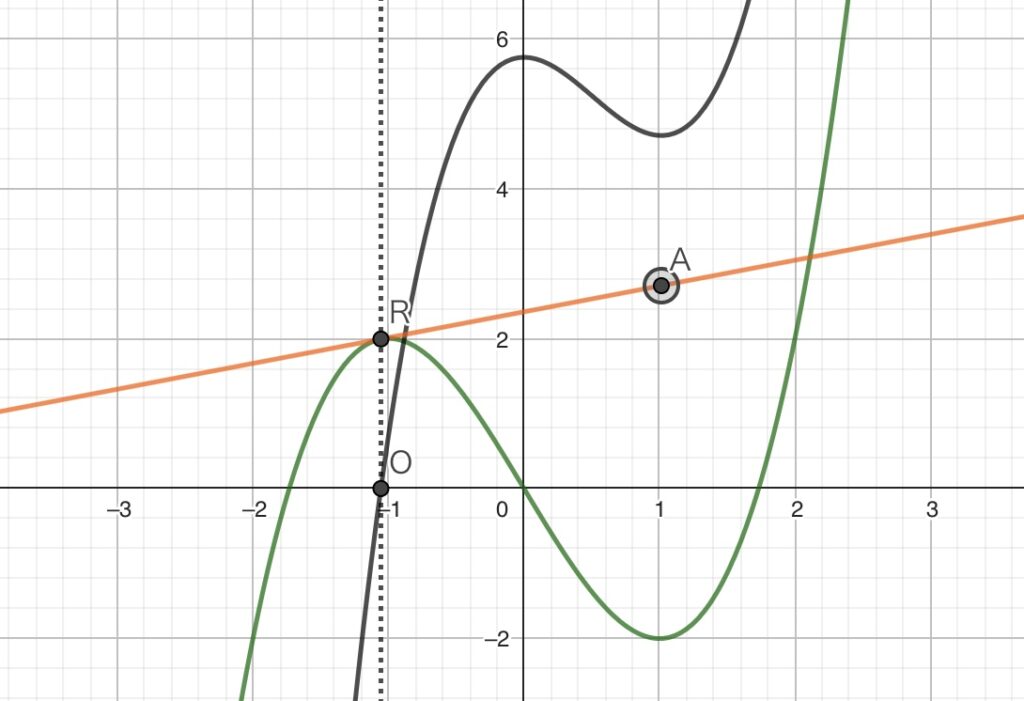
このようにGeoGebraで点を動かしながらグラフを描いていくと、接線の本数が\(p(x)=0\)の解の数と一致することが理解できると思います。
実数解が3つになる条件を考える
接線の本数が\(p(x)=0\)の解の数と一致するため、この問題の鍵は\(p(x)=0\)の解の数です。GeoGebraのようなグラフ計算機ツールを使えるのであれば解の個数を調べる方法はいくらでもありますが、もともとこれは大学受験の問題。手計算でも解ける方法を選択しなければいけません。そのため、荻野先生の講義では\(p(x)\)の極値の符号を調べる方法を解説しています。
さて、GeoGebraには極値を計算するツールがあります。ここではこのツールを使って関数\(p(x)\)の極値をプロットしてみましょう。
極値ツールを使ってみた結果がこちらです。ここでは点U、点Vという点で極値が示されています。
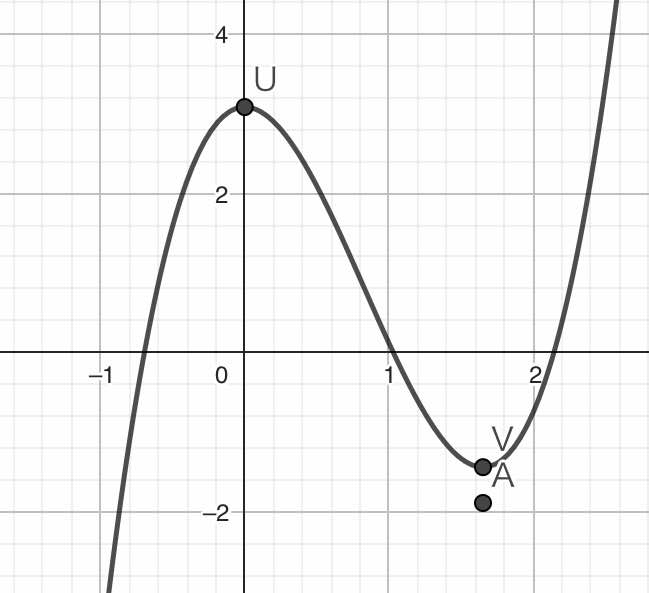
関数\(p(x)\)の極値とは\(p(x)\)の傾きがゼロになる点、言い換えると\(p’(x)=0\)となる点のことです。ここでは\(p(x)=2x^3 -3 a x^2 +(3a + b)\)ですから、両辺微分すると\(p’(x)=6x^2 -6 a x\)となります。\(p’(x)=0\)は\(x(x-a)=0\)に変形できますから、\(p’(x)=0\)の解は\(x=a,0\)の2つということになります。したがって、関数\(p(x)\)の極値は\((a,p(a))\)、\((0,p(0))\)の2点です。上の図をみて、極値が\((a,p(a))\)、\((0,p(0))\)の2点になっていることを確認してください。
先ほどの図では極値U、Vの\(y\)成分の符号がそれぞれ異なっていました。つまり、極値Uの\(y\)成分はプラス、極値Vの\(y\)成分はマイナスです。このような場合、\(p(x)=0\)は3つの実数解を持ちます。
この極値の符号に関する条件が満たされない場合、\(p(x)=0\)の実数解の数は1個(もしくは2個)になります。例えば、以下の図のように点Aを移動させてみると、\(p(x)=0\)の実数解の数は1個になり、極値Uのy成分と極値Vのy成分はどちらもプラスになります。点Aの位置によっては、どちらの符号もマイナスになることがありますが、極値Uのy成分と極値Vのy成分の符号が同じ場合、基本的に\(p(x)=0\)の実数解の数は1個です。
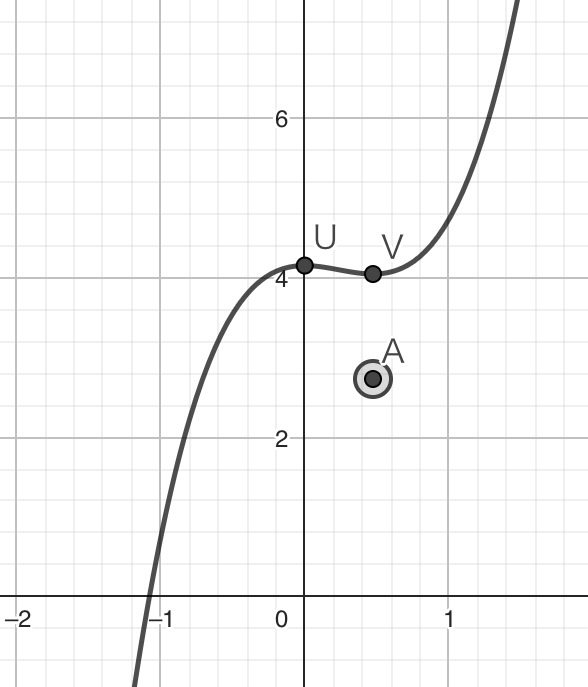
例外的に極値U、Vのy成分のいずれか一方だけがゼロとなるケースでは\(p(x)=0\)の実数解の数は2個になります(いずれかの解が重解となるため)が、それを除けば、\(p(x)=0\)の実数解の数は1個もしくは3個になります。
ここで\(p(x)=0\)の実数解が3つ存在するための条件を整理しましょう。\(p(x)=0\)の実数解が3つ存在するためには、\(p(a) \neq 0\)かつ\(p(0) \neq 0\)であり、さらに\(p(a)\)と\(p(0)\)の正負の符号が異なっている必要があります。この条件は\(p(a) \cdot p(0) < 0\)というシンプルでエレガントな式で表すことができます。
条件を満たす範囲を図示する
あとは\(p(a) \cdot p(0) < 0\)という不等式の範囲がグラフ上のどこに該当するかを示せば良いです。ここでは\(p(x)=2x^3 -3 a x^2 +(3a + b)\)ですから、\(p(a)\)と\(p(0)\)は以下のように書けます。
$$\begin{align}
p(a) &= 2a^3 -3 a^3 +(3a + b)=-a^3 +3a + b\\
p(0) &= 3a + b\\
\end{align}$$
ここで\(a=x\)、\(b=y\)に変数を置き直すとともに、式をすこし冗長な形に変形してみましょう。\(p(a) \cdot p(0) < 0\)という不等式は以下のような形で表すこともできます。
$$\begin{align}
((y > x^3 -3x ) &\wedge (y<-3x))\\
&\lor \\
((y < x^3 -3x ) &\wedge (y>-3x))\\
\end{align}$$
ここで、\(\wedge\)は論理積(AND演算、かつ)を、\(\lor\)は論理和(OR演算、または)を意味します。
そして、上の不等式をGeoGebraで描画した結果が、下記の画像です(※この記事の前半部に掲載した画像を再掲)。

これで、この問題に関する予想が正しかったことをようやく証明できました(長かった……)。
ちなみに、「\(y=-3x\)というグラフ、どこかで見覚えが……」と思ったアナタは鋭い。以下の図はこの記事の前半部に掲載したグラフを再掲したものです。

三次関数\(y=x^3\)と一次関数\(y=-3x\)を足し合わせたものが、この問題で取り扱った三次関数\(y=x^3-3x\)でした。この記事の前半部に出てきた何気ない一次関数がこの問題の答えと深く関連しているところが興味深いですよね。
ちなみにですが、この問題で取り扱った三次関数\(y=x^3-3x\)を二階微分すると、さらにおもしろいことがわかります。二階微分の結果は\(\frac{\mathrm{d}^2 y}{\mathrm{d} x} = 6x\)ですが、ここで\(\frac{\mathrm{d}^2 y}{\mathrm{d} x} = 0\)となる点を調べてみると、\(x = 0\)という式が出てきます。さて、\(x = 0\)で三次関数\(y=x^3-3x\)と接する接線の方程式は……そうです、\(y=-3x\)です。二階微分をすると任意の点を通過する接線の本数が変わる境界線がわかるというのはおもしろい知見ですね。
このように接線の問題を考えるときに微分はとても重要なわけです。
余談 〜四次以上の関数の接線〜
ここから先は余談と言いますか、瑣末な話です。荻野先生の講義では4次以上の関数に対しては同じ考え方だと答えが出せないと言っています。4次以上の関数では二重接線や三重接線が存在しうるため、そう簡単にはいかないのだと。「所詮、手際よく解けるように作られた入試問題という 箱庭の中でしかぁー、いっ、生きていけない解答に過ぎないんだ。」だと。
受験数学は手計算で解けない問題は出題されないため、荻野先生の発言には一理あります。しかし、実は4次以上の関数でもほとんど同じ考え方で答えが出せるのです(詳細は別の記事で説明します)。確かに二重接線や三重接線が存在する可能性があるため、場合分けが少し複雑になります。ただ、受験で4次以上の関数の接線の問題が出ないのは、普通、3次以上の方程式は手計算だと解けないためです。4次以上の関数に対して同じような接線の問題を考えると3次以上の方程式を考えないといけない場面が出てくるのですが、これが手計算では普通、解けません。受験数学では手計算で解けない問題が出ることはありませんから、4次以上の関数の接線の問題は出さない、ということになっているのだと思います。
仮に、うまく解ける問題を作ることができたとしても、4次以上になると複雑性が増すだけで、解いた後の納得感や爽快感はさほど増えません(残念)。そういう問題はあまり良い問題とは思えないですね。その点、この問題は上手くできているなと感心しました。良い問題です。
まとめ
この記事では、無料の数学ソフトGeoGebraを使って、代々木ゼミナールの荻野暢也先生が解説していた接点tの問題を詳細に解説してみました。大手予備校で解説されていた難問ですが、逐一グラフを描いてみると、比較的理解しやすいのではないかと思います。答えも綺麗で、とても良い問題だなと感じます。
次回の記事では4次以上の関数に対して同じような問題を考えてみたいと思います。4次以上の関数に対して同じアプローチが通用するのか、詳細に検討してみましょう。















