いくつか前の記事から、GeoGebraのオブジェクトについて説明しています。なお、この記事はGeoGebra公式サイト(オブジェクト関連ページ)をもとに作成されています。
GeoGebraのオブジェクトには一般的なものと幾何学的なものの2種類があります。今回の記事は、前回の記事に引き続き、幾何学的なオブジェクトについて説明していきます。
直線と座標軸
まずは直線オブジェクトについて説明します。
ツールによる幾何オブジェクトの描画
GeoGebraには幾何オブジェクトを描画するための様々なツールがあります。例えば、直線を引くツールだけでも以下のものがあります。
- 2点を結ぶ線分
- 2点を通る直線
- 垂線
- 垂直二等分線
- 平行線
- 角の二等分線
- 接線
- 長さを指定した線分
- 2点を通る半直線
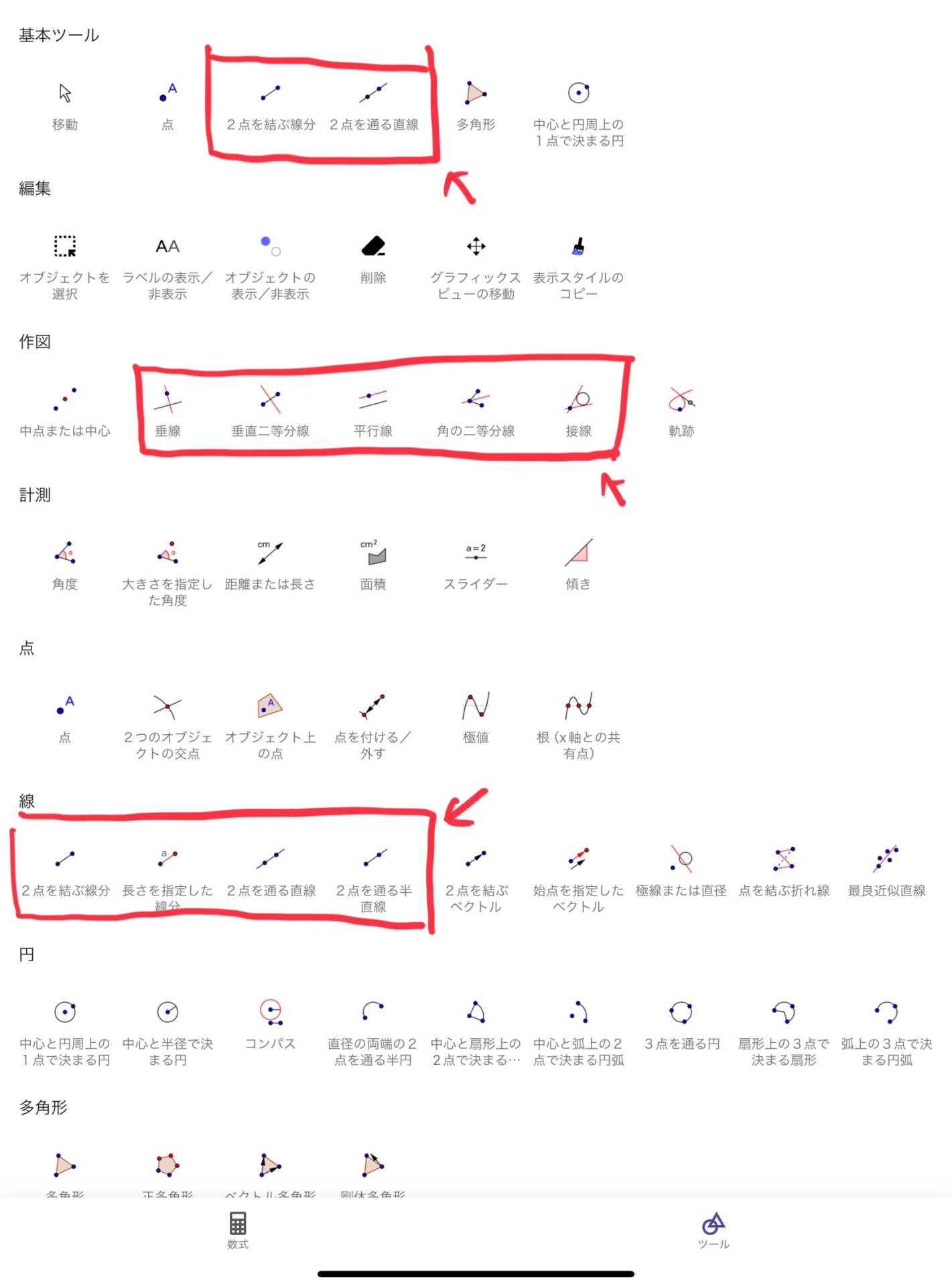
これらのツールももちろん便利なのですが、数式やコマンドを用いて幾何オブジェクトを描画することもできます。この記事では主に数式やコマンドによる幾何オブジェクトの描画方法について説明します。
数式による直線の描画
GeoGebraの良いところの一つは、直線や曲線の方程式を入力すると瞬時にそのグラフを出力できるところです。こういったソフトウェアのことを「グラフ計算ソフト」といいます。
基本的な描画方法
最も有名な形のxy平面上における直線の方程式は\(y=ax+b\)ですが、まずはこれをそのままGeoGebraに入力してみましょう。
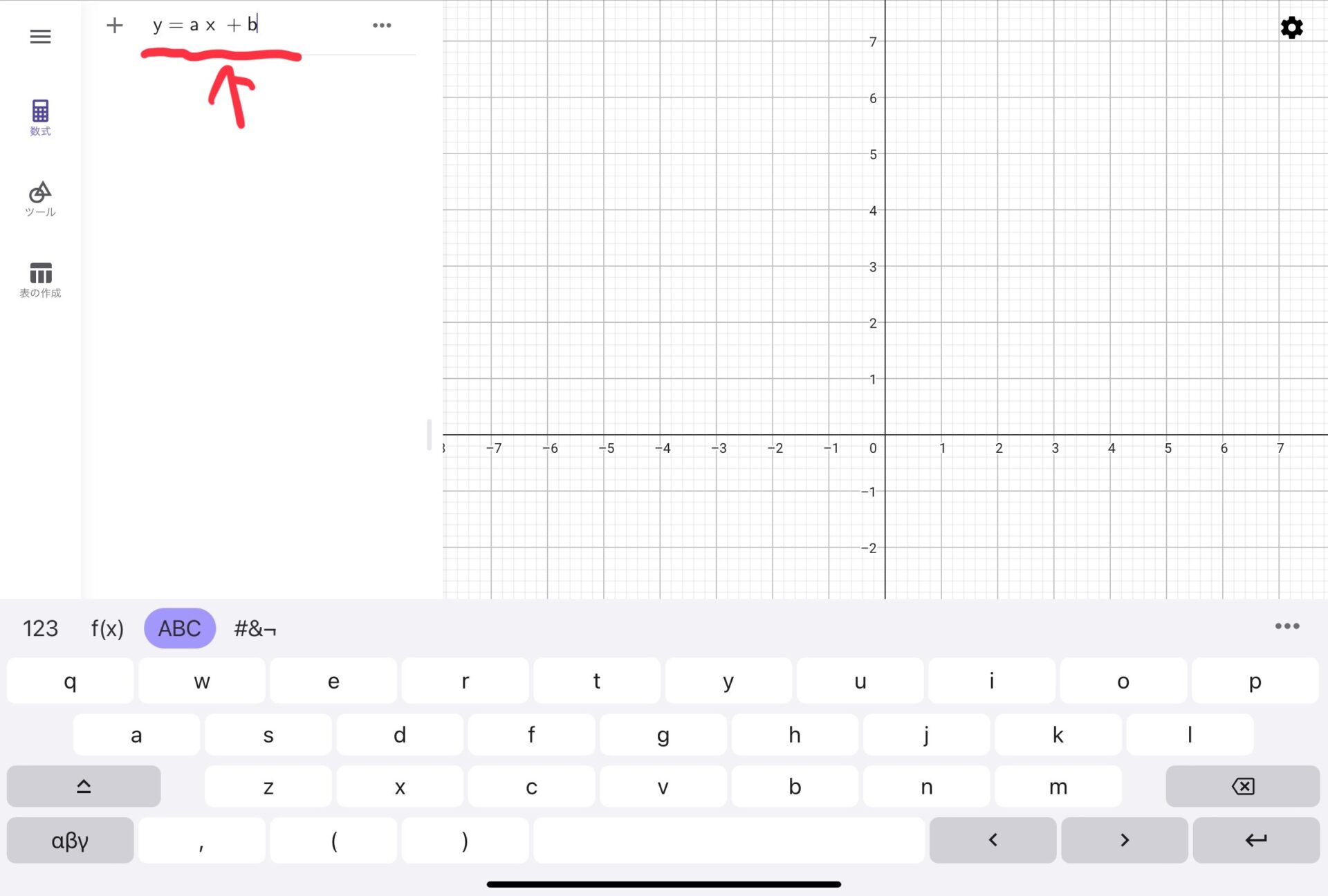
すると、画面が以下のように変化します。
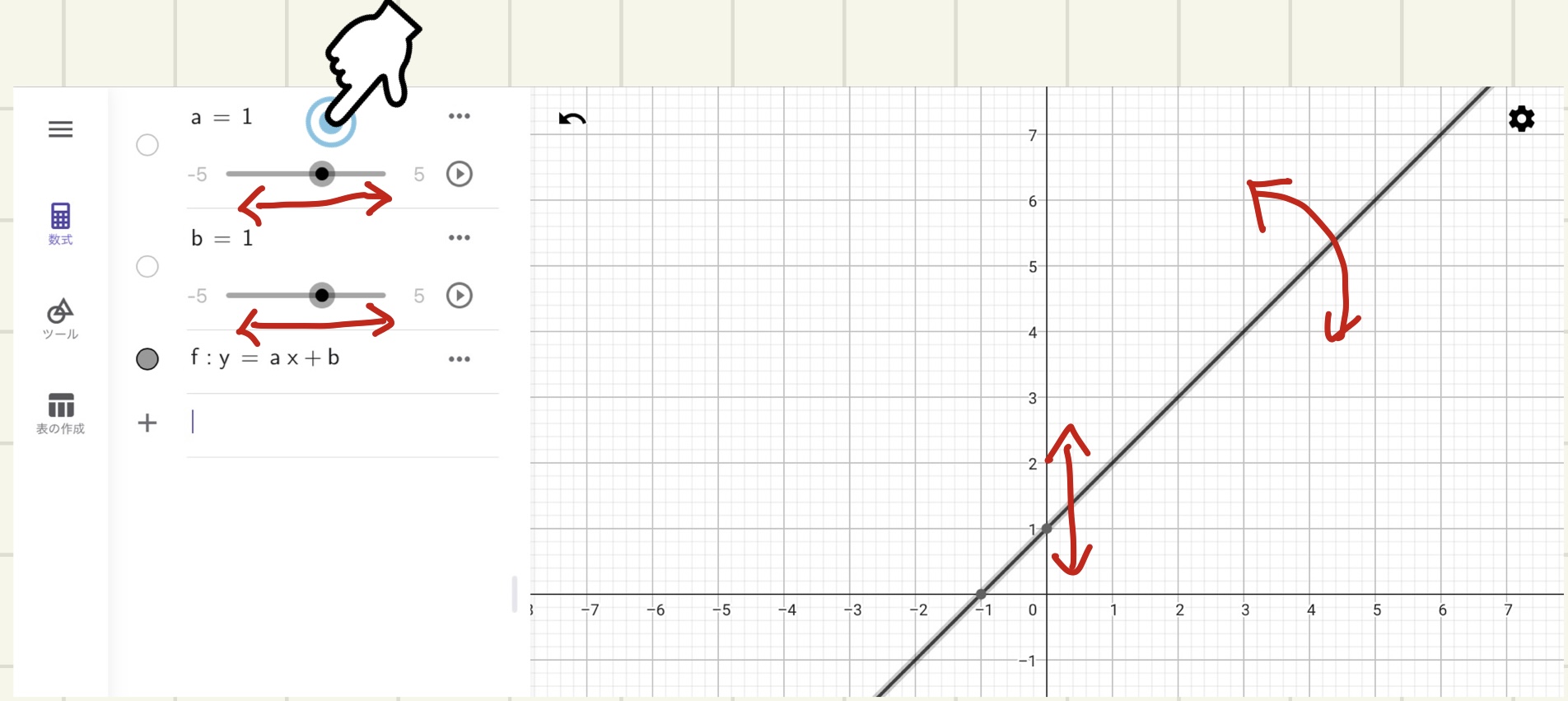
\(a,b\)という定数を設定するためのスライダーが現れ、画面上に一本の直線が描画されました。ここでは、\(a=1,b=1\)が初期値として代入されていますので、描画される直線は\(y=x+1\)です。スライダー機能を使って、\(a,b\)という定数を変化させると、グラフの傾きや切片が連動して変化します。
なお、上記の例では直線オブジェクトに対し、fという名称が自動的に設定されています。直線オブジェクトに対して自分で名前をつけたい場合は、:(コロン)を使用してください。
このようにワンアクションでグラフを描けるのがGeoGebraの良いところなのです。
媒介変数表示での描画方法
GeoGebraに対して媒介変数表示の数式を入力することもできます。例えば、\(x=1+3t, y=1+t\)という数式をGeoGebraに入力してみます。媒介変数\(t\)を消去すれば、これは普通の直線の方程式です。まずは点を入力するときのように(1+3t, 1+t)と入力します。
すると、以下のように直線が描画されました。
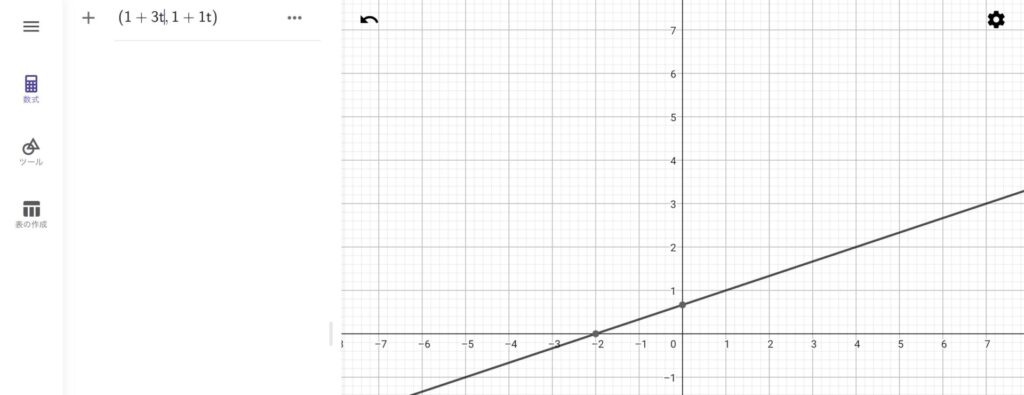
点とベクトルと媒介変数\(t\)を用いて直線を表現することもできます。任意の点\(A\)と方向ベクトル\(v\)があった時、直線は\(A+v t\)という数式で表現できます。これをGeoGebraに入力してみましょう。例えば、さきほどと同じ直線を引くためには以下のように入力します。
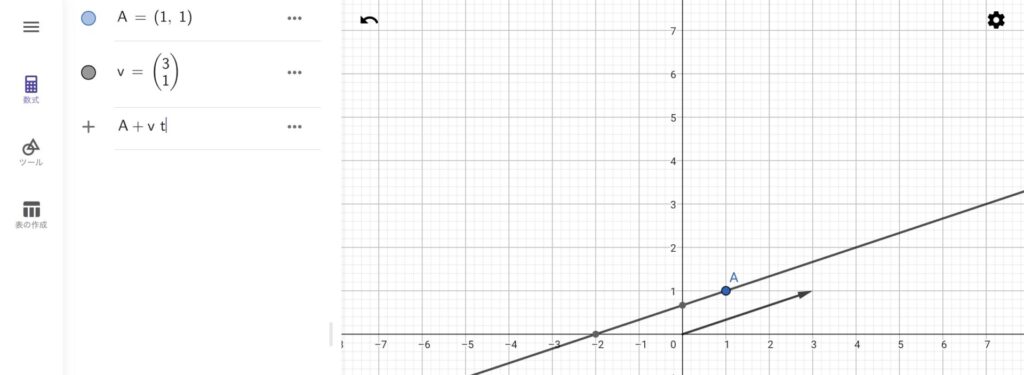
先ほど同じ直線が引けました。ちなみにA+v tの代わりにLine(A,v)と入力しても同じ結果が得られます。
直線の方程式はさほど難しくないので媒介変数表示のメリットはあまりありませんが、複雑な曲線を取り扱う場合は媒介変数表示はとても便利です。これについては後で詳しく説明しましょう。
座標軸の参照方法
数式やコマンドを活用してグラフを作成する場合、xyの座標軸を参照したいことがあります。そういった場合はxAxisと yAxisという入力すれば良いです。
例えば、垂線を引くためのコマンドPerpendicularLineを使用する場合、PerpendicularLine(A, xAxis)などと入力します。すると、点Aを通り、x軸と垂直な線を引くことができます。
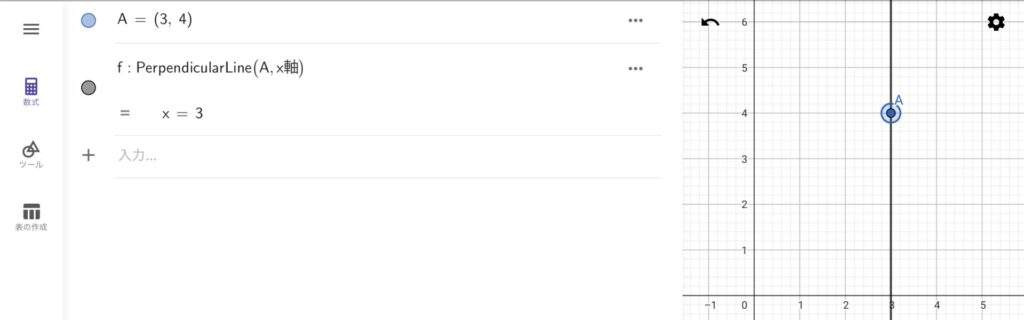
なお、日本語環境ではxAxisと入力した後にEnterを押すと、x軸に表示が変わります(上の図でも変わっています)。
直線の係数の取得
x( ),y( ),z( )コマンドを\(xyz\)の3次元平面上の直線オブジェクト\(ax+by+cz=d\) (ただし、\(a,b,c,d\)は実数)に対して作用させた場合、変数\(x,y,z\)の係数\(a,b,c\)を取得することができます(※2次元平面上の直線に対しても同じように係数を取得できます)。使用例を以下に示しますので、ご興味のある方は確認してみてください。
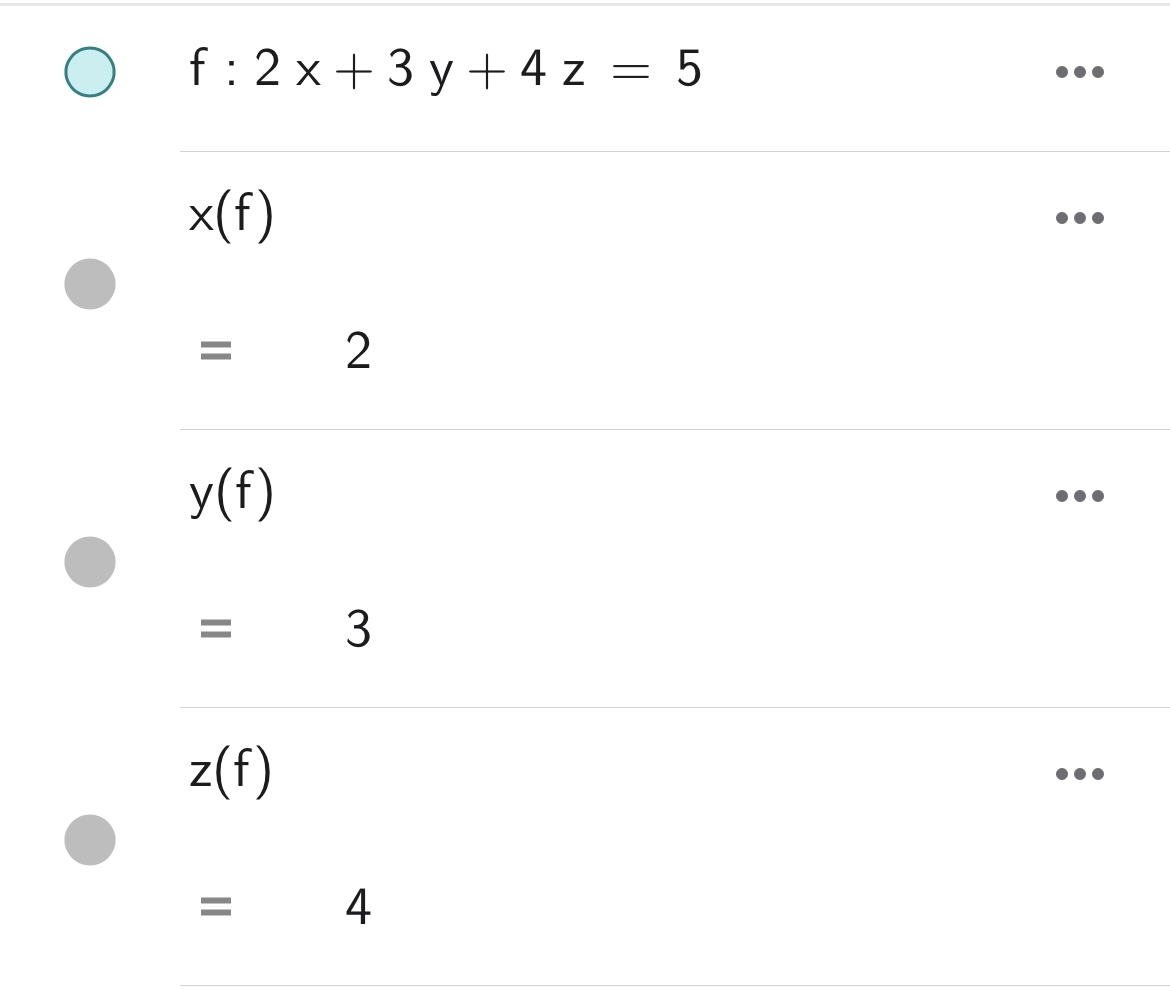
円、楕円、双曲線、放物線
GeoGebraは円や楕円、双曲線、放物線を描画するのも得意です。数学の世界では円や楕円、双曲線、放物線のことをひとまとめにして「円錐曲線」と呼びます。
円錐曲線とは?
なぜ円や楕円、双曲線、放物線を「円錐曲線」と呼ぶのかについて、簡単に説明しておきましょう。まず、2つの円錐を下記のように配置するとします。
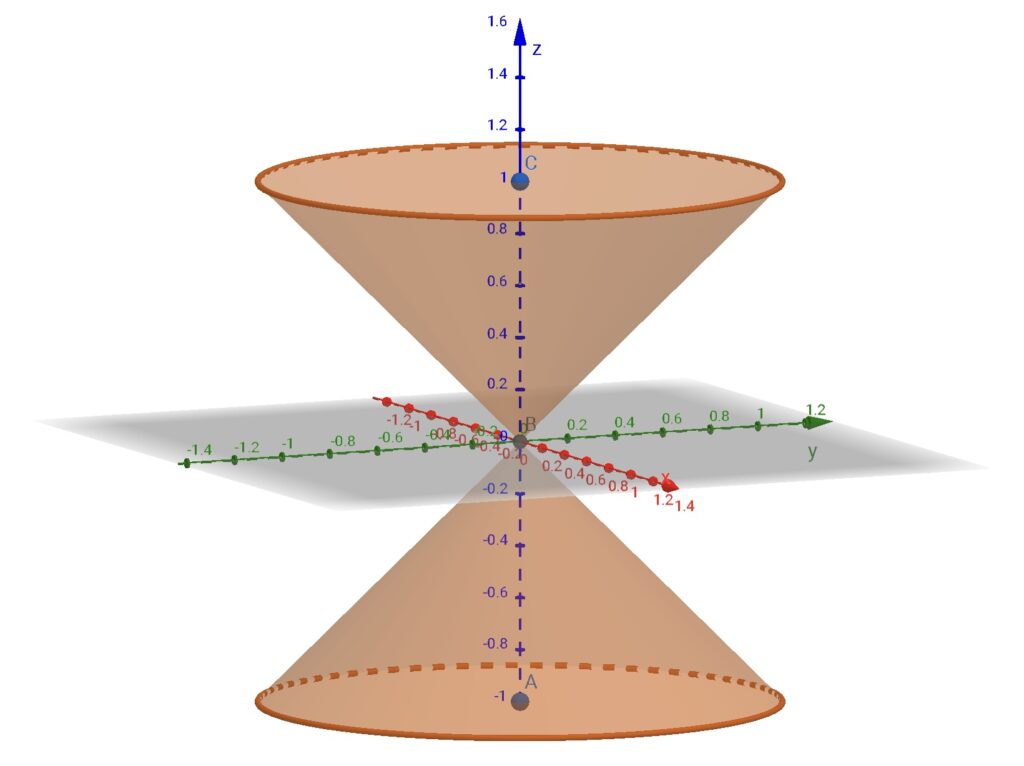
なんとなく砂時計のような形をしていますね。なお、ここでは作画の都合上、円錐の高さは有限ですが、理想的には円錐の高さは無限大であるとします。
ここで少し唐突ではあるのですが、適当な平面で2つの円錐をスパッと切断することを考えてみましょう。切断した時に現れる断面の形はどうなるでしょうか?(少し読むのを止めて、考えてみてください。)
例えば、以下の例ではカットした断面が楕円状になっています。
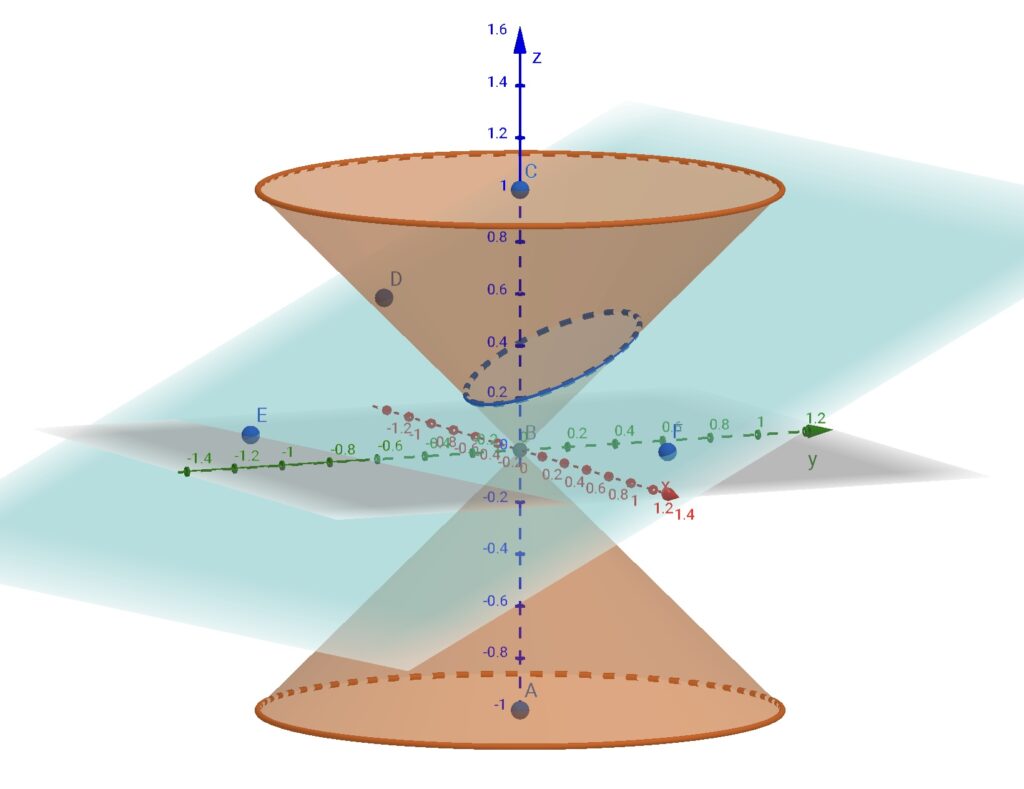
こちらの例では、双曲線状になります。
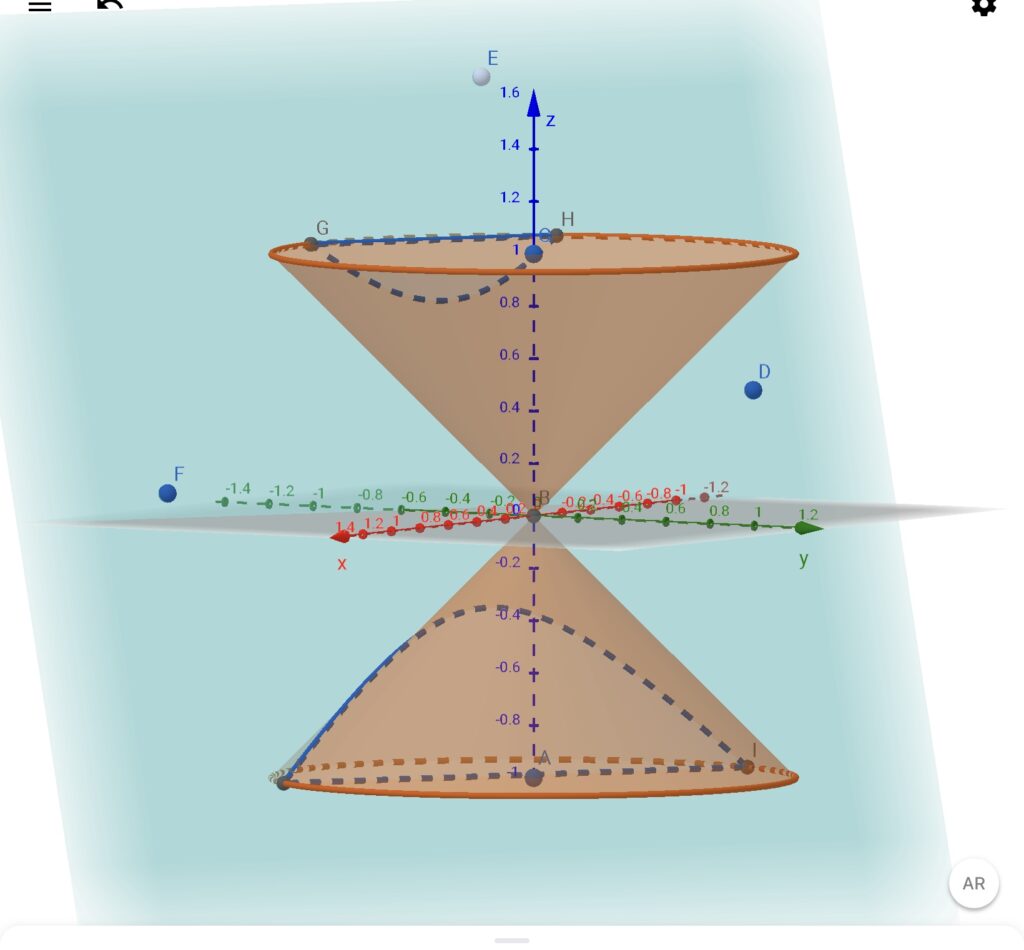
真円になる例と放物線になる例は示しませんが、どうやら先ほどの砂時計をうまく切断すると、円や楕円、双曲線、放物線が作れそうです。このことから、数学の世界では円や楕円、双曲線、放物線のことをひとまとめにして「円錐曲線」と呼ぶのです。
円と楕円の描画例
GeoGebraでは円や楕円の方程式を入力すると、自動的に円や楕円のグラフが描画されます。例えば、\({\frac{x}{a}}^2+{\frac{y}{b}}^2=r^2\)と入力してみましょう(ただし、\(a,b,r\)は正の定数とする)。
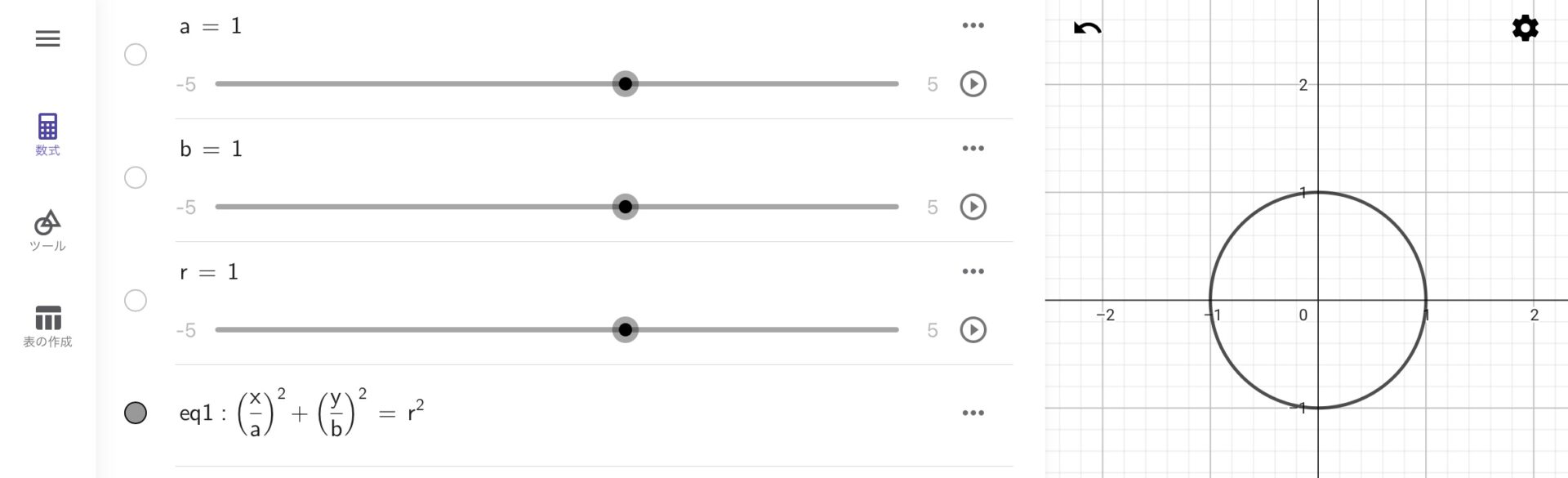
\({\frac{x}{a}}^2+{\frac{y}{b}}^2=r^2\)と入力すると\(a,b,r\)に関するスライダーが作られるとともに、円が描画されます。また、スライダー機能を使って\(a,b\)を変化させると、楕円になります。
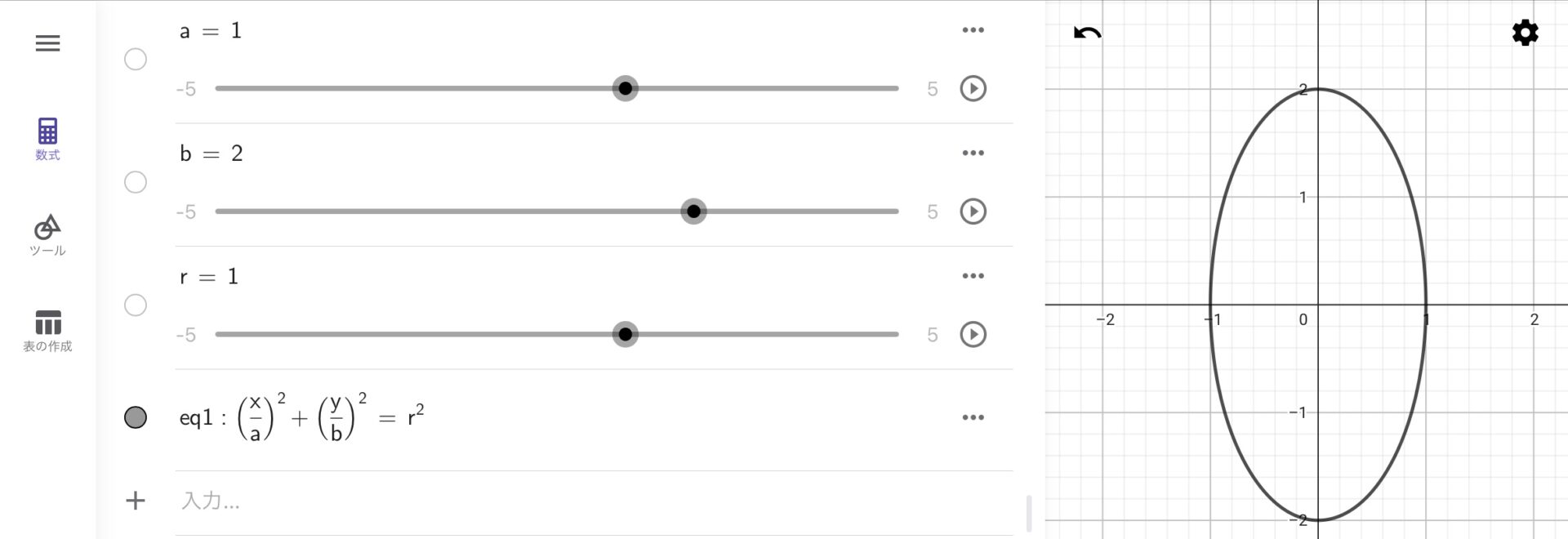
なお、GeoGebraでは媒介変数を利用して、円を描くこともできます。\((\cos(t), \sin(t))\)と入力してみてください。

双曲線の描画例
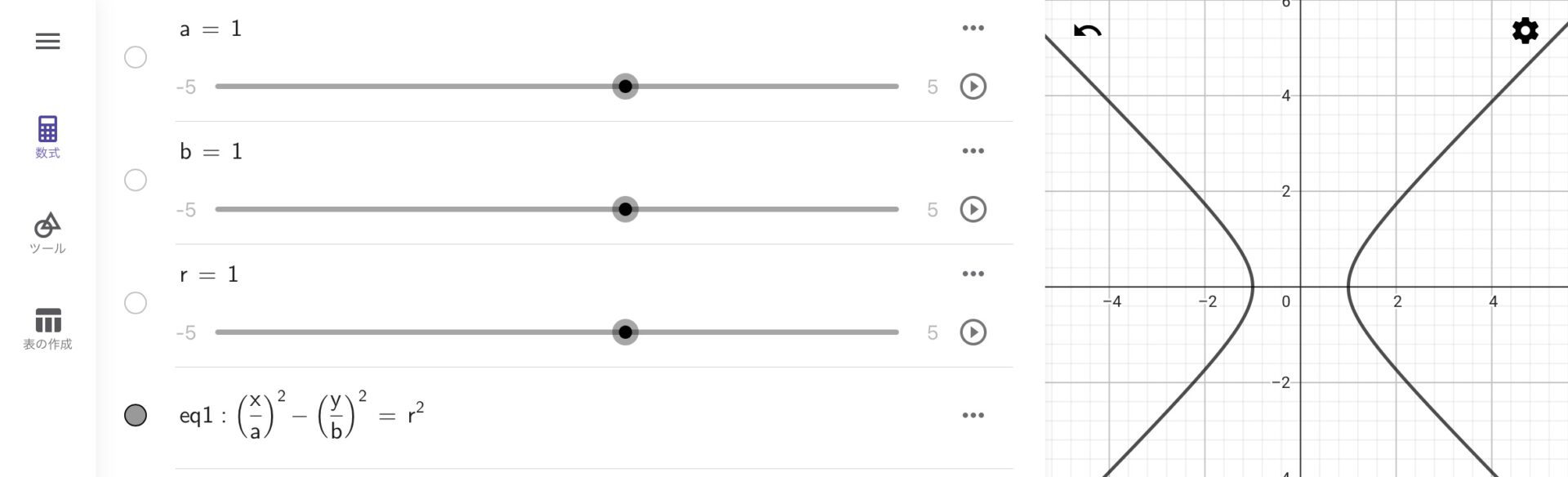
次は双曲線を描いてみましょう。\({\frac{x}{a}}^2-{\frac{y}{b}}^2=r^2\)と入力してみてください(ただし、\(a,b,r\)は正の定数とする)。すると、以下のグラフが描けます。
放物線の描画例
最後に放物線です。\({\frac{x}{a}}^2-y=r^2\)と入力してみてください(ただし、\(a,b,r\)は正の定数とする)。すると、以下のグラフが描けます。

このようにGeoGebraでは数式を入れるだけで円錐曲線をワンアクションで描くことができます。
まとめ
この記事では、GeoGebraで直線や円錐曲線を描く方法を説明しました。職場や学校ではMicrosoft Excelのような表計算ソフトがよく使われていますが、GeoGebraのようなグラフ計算ソフトが表計算ソフトと違うのは、ワンアクションでグラフを描くことができるという点です。陰関数の形や媒介変数を用いて記述された関数もワンアクションでグラフ化できるのはとても爽快です。
GeoGebraは数学を学ぶ際にとても便利なソフトウェアなので、ぜひ使ってみてください。そして、あなたの数学への理解度をアップさせてください。






